Misterios del número π

Resumen

El número π es de mucha utilidad en diversas ramas de la ciencia y la ingeniería y este ha sido usado desde hace milenios en el desarrollo de infraestructuras de ciudades, construcción de puentes, cálculos de distancias y otras cantidades; sin embargo, existen aún muchas incógnitas que, si bien se asumen verdaderas por comprobaciones numéricas de casos particulares, no se han logrado demostrar. En este artículo se hará una revisión sobre la historia del número π, incluyendo el famoso problema de la cuadratura del círculo con el fin de entender algunas de sus características, para finalmente revisar algunos de los problemas que aún siguen abiertos.
Palabras clave: Número pi, números irracionales, números normales, series.

Mysteries of number π

Abstract

The π number is very useful in various branches of science and technology and it has been used for millennia in the development of city infrastructures, bridge construction, distance measures and other measurements. However, there are still many questions that although they are assumed to be true by numerical checks of particular cases, they have not been proven. In this article we will review the history of the π number, including the famous quadrature of the circle problem with the objective to understand some of the characteristics of number π, to finally review some of the problems that are still open.
Keywords: Number pi, irrational numbers, normal numbers, series.

Introducción

Durante la educación básica, en matemáticas, los niños aprendes a calcular el área de diferentes “figuras geométricas”, por ejemplo: cuadrados, rectángulos y círculos. Estos cálculos son útiles debido a las diversas aplicaciones en la vida cotidiana, como saber el tamaño de una superficie, por mencionar una.

La primera área que se aprende a calcular es la del cuadrado que es simplemente el cuadrado (es decir, la multiplicación del número por sí mismo) de la longitud de su lado $(área=l^2)$. Esta fórmula es tan intuitiva que no requiere de una demostración y la aceptamos como la definición.

Para otras figuras, calculamos su área por la suma de las áreas de cuadrados pequeños que la cubren. Así, dividiendo un rectángulo en pequeños cuadrados, es fácil ver que el área total de este será: $área=bxh$, dónde $b$ es la longitud de la base del rectángulo y $h$ su altura.

Otras fórmulas que se estudian son aquellas con las que se calculan las áreas del triángulo, el rombo, el trapezoide y el círculo. El caso del círculo aparece una “extraña” constante, $\mathrm{\pi }=3.14$. La fórmula para estimar el área de éstos es: $\mathrm{área}={\mathrm{\pi r}}^2$, donde r es el radio del círculo. Por lo regular no se explica de dónde sale esta ecuación, lo único que se enseña es que π es el valor de la circunferencia1 de un círculo de radio 1, la cual se puede medir dibujando un círculo con un compás y midiendo la longitud de un hilo que cubra la circunferencia. La relación entre el área de un círculo y su diámetro se puede entender si se aproxima al círculo por polígonos regulares de muchos lados. En este caso, el área del círculo es aproximadamente el área del polígono (ver figura 1a), mientras que su perímetro es aproximadamente la suma de los de los lados.

El polígono se puede dividir en tantos triángulos isósceles como lados tenga. Si se acomodan adecuadamente estos triángulos, podemos calcular el área del polígono como lo haríamos con la de un rectángulo cuya base es aproximadamente $\mathrm{r}$ y la altura es la mitad del perímetro del polígono que, a su vez, es más o menos la mitad del perímetro del círculo (ver figura 2b), es decir $\mathrm{\pi r}$. Al multiplicar la base ($~\mathrm{r}$) por la altura ($~\mathrm{\pi r}$) de este rectángulo obtenemos su área, que es el área del polígono que a su vez es aproximadamente el área de un círculo (${\mathrm{\pi r}}^2$).

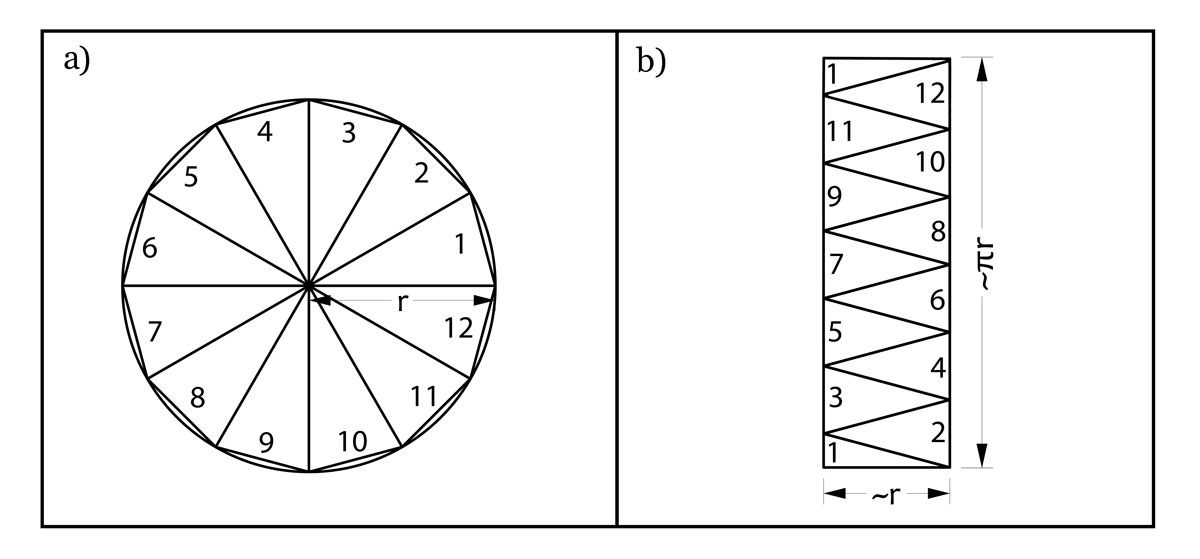
Figura 1. Esquema de la demostración de que el área de un círculo es πr². En (a) el círculo ha sido aproximado por un polígono de 12 lados. Este polígono está compuesto por 12 triángulos isósceles iguales. En (b) Los mismos 12 triángulos han sido acomodados para formar un rectángulo de base ~r y altura ~πr.

Cuadratura del círculo

El primer método del que hablamos para estimar π (el que usa un hilo) mide directamente la circunferencia, la cual podemos dibujar con un compás. El problema de este método es la dificultad representa la precisión al medir la longitud del hilo, ésta se incrementa si el tamaño de la circunferencia es mayor, el problema es que entre más grandes son los círculos, es más difícil dibujarlos y por lo tanto poco precisos. Por esta razón, la mayoría de las culturas en la antigüedad hicieron estimaciones inexactas; casi siempre consideraban $\mathrm{\pi }=3$.

Medir el área de un cuadrado suele ser más sencillo que medir el área o perímetro de un círculo y por lo tanto también suele ser más preciso.; por ello, podríamos pensar que un mejor método sería medir el área de un cuadrado de lado $|=\sqrt{\pi }$. El problema de este método es dibujar un cuadrado con esa característica. Para trazar figuras geométricas con mucha precisión, los dos instrumentos por excelencia son el compás y la regla.2 Entonces, primero debemos preguntarnos ¿Cómo construir, con regla y compás un cuadrado cuya área sea la de un círculo de radio 1?, de tal manera que medir su área sea medir π. A este problema se le conoce como la cuadratura del círculo y su solución no es para nada intuitiva;3 tanto así, que se convirtió en uno de los problemas más desafiantes en la historia de las matemáticas. Los primeros en tener avances significativos al respecto fueron los egipcios (Petrie, 1940), 1800 años a.C. Ellos descubrieron que el cuadrado que medía 16/9 de unidades por lado tenía un área muy similar al de un círculo de radio 1.4 Con esto aproximaron la constante π como $\mathrm{\pi }=\frac{256}{81}~3.16$, la cual se volvió una de las mejores aproximaciones de la antigüedad y cuyo descubrimiento tardó más de mil años en ser rebasado.

A lo largo de la historia hubo miles de intentos por resolver la cuadratura del círculo y un sinfín de propuestas sobre cómo construir (erróneamente) un cuadrado con área igual a la de un círculo dado. No fue sino hasta 1882, que el matemático alemán Lindermann logró resolver el misterio al demostrar la imposibilidad de dicha construcción; es decir, el problema se mantuvo abierto por más de 3 mil años, uno de los problemas matemáticos que más tiempo han estado sin resolverse. Como éste duró tanto tiempo sin solución, adquirió fama y llamó la atención de matemáticos aficionados. Hay publicaciones que tratan de demostrar, de forma errónea, las cuadraturas del círculo, al menos hasta 1894 (Goodwin, 1894).

Aproximación de Arquímides

Desde el trabajo plasmado en el papiro de Rhind, donde se muestra la aproximación a π como 3.16, no hubo avances sustanciales en esta constante, sino hasta la época de Arquímides (Arndt y Haenel, 2001), quien alrededor del año 250 a.C. aproximó el perímetro del círculo de diámetro 1 mediante polígonos, tal como se muestra en la figura 2a, tomando tanto la aproximación inferior, como la aproximación superior. El algoritmo de Arquímides dio pie a una serie de mejoras en la aproximación de π que llegó hasta 16 dígitos decimales de precisión para el año 1593 por Adrianus Romanus (Schepler, 1950). Por la importancia del cálculo de Arquímides, se explicará brevemente la aproximación inferior, aunque ello requiere de un esfuerzo mental elevado.

Primero notamos que si uno construye un hexágono inscrito en un círculo (dentro del círculo, pero cuyos vértices forman parte de la circunferencia), podemos dividir éste en 6 triángulos equiláteros (ver figura 2), cuyo lado es un radio, por lo tanto, el perímetro del hexágono será simplemente $6r_{}$. Si $r=\frac{1}{2}$, el perímetro será 3, que es nuestra primera aproximación de π. La siguiente aproximación, consiste en pasar a un polígono de 12 lados. Para esto, sobre cada uno de los lados del hexágono insertamos un triángulo isósceles, cuya base sea un lado del hexágono que llamaremos $l_6=r$ de forma que el otro vértice quede sobre la circunferencia. Como el triángulo es isósceles, cada uno de los lados de la envolvente será del mismo tamaño, formando un polígono regular de 12 lados. Sabemos que la distancia del centro de la circunferencia a cualquiera de los vértices de nuestro polígono es un radio. Por lo tanto, la altura del triángulo isósceles será simplemente $h_{12}=r–L_6$, donde $L_6$ es la apotema del hexágono (la distancia del centro del círculo al centro de uno de los lados del hexágono). Para calcular $L_6$ podemos usar el Teorema de Pitágoras, obteniendo $L_6=\sqrt{r^2–\frac{1}{4}{r}^2}=\sqrt{3}\frac{r}{2}$. Una vez más usamos este teorema para calcular el lado $l_{12}$ del polígono de 12 lados, pues tenemos la altura $h_{12}$ del triángulo isósceles y su base $l_6=r$, por lo tanto $l_{12}=\sqrt{\raisebox{1ex}{$l_{26}$}\!\left/ \!\raisebox{-1ex}{$4$}\right.+h_{12}^2}$. Repetimos este proceso una y otra vez simplemente sustituyendo $l_6$ por $l_{3\times 2}n$ para después calcular $L_{3\times 2^n}$, $h_{6\times 2^n}$ y finalmente $l_{6\times 2^n}$.

Arquímides repitió este procedimiento 4 veces y obtuvo primero el polígono de 12 lados, después de 24, 48 y finalmente 96 lados. Aproximando las raíces cuadradas que obtenía por fracciones, pudo demostrar que $\mathrm{\pi }>\frac{223}{71}$ y ya antes había mostrado, usando un procedimiento similar, pero con polígonos circunscritos (por fuera de la circunferencia), que $\mathrm{\pi }<\frac{22}{7}$. Es decir, pudo acotar el valor de π entre $\frac{223}{71}$ y $\frac{22}{7}$, lo cual mejoró la aproximación de los egipcios; pero, más importante aún, creó un algoritmo con el que en principio podía aproximarse tanto como se quisiera el valor de π.

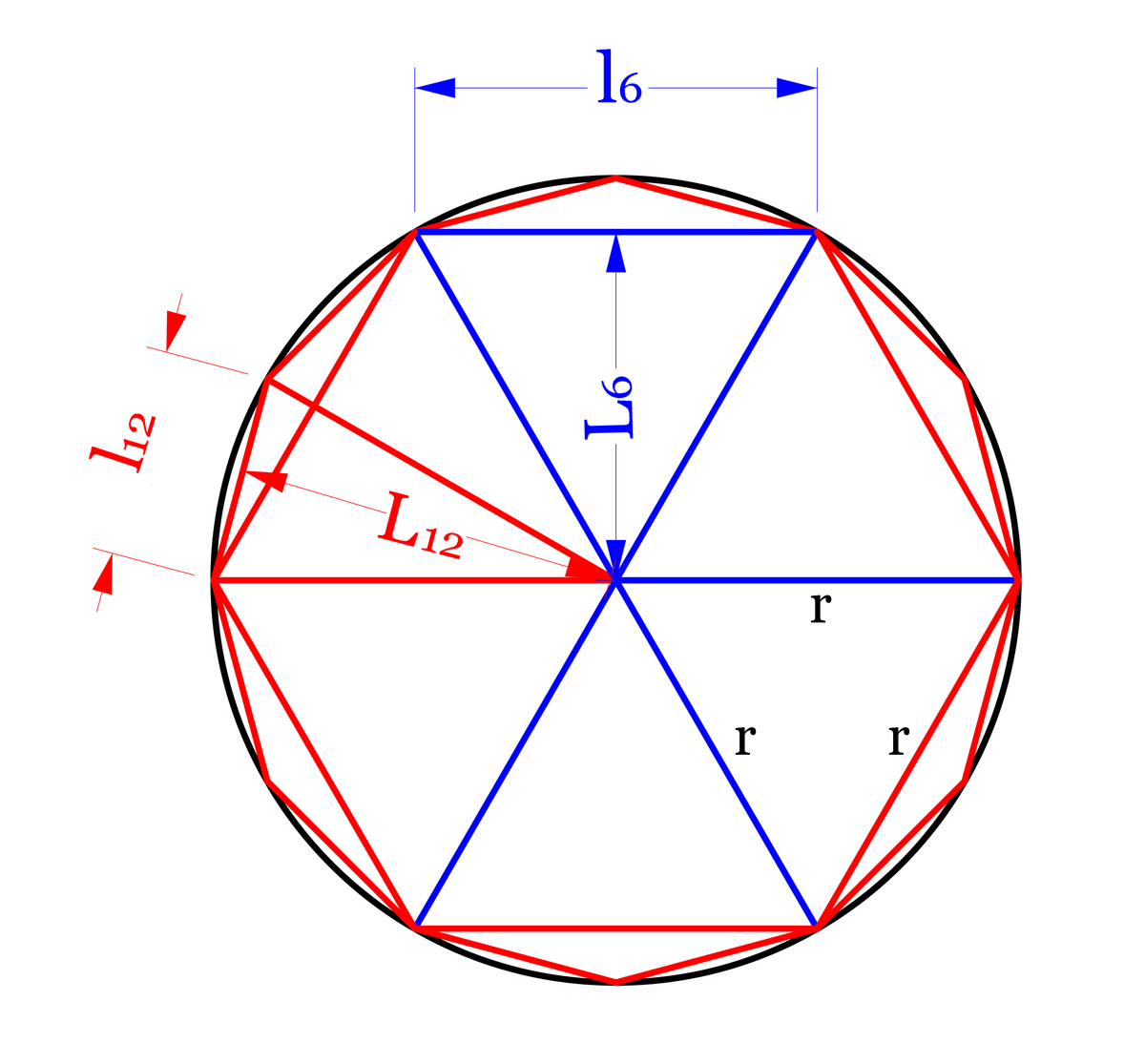
Figura 2. Esquema para desarrollar el algoritmo de Arquímides para el cálculo de π.

Otras definiciones de π

Después de Arquímides hubo muchos matemáticos que intentaron crear mejores algoritmos para calcular π a través de muchos esfuerzos por modificar la definición de la constante, mostrando equivalencias con la definición original. Hay un sinfín de posibles definiciones de π, cada una de ellas relacionada con alguna fórmula matemática o física importante. Mencionaremos sólo algunas de ellas.

Una interesante definición se la debemos a Euler (Posamentier y Lehmann, 2004), quien encontró que la probabilidad de que dos números naturales cualesquiera sean primos relativos5 está dada por $p=\frac{6}{n^2}$, con lo que se pudo definir más tarde a la constante en función de la probabilidad de que dos números sean primos relativos $\mathrm{\pi }=\sqrt{\frac{6}{\mathrm{p}}}$. La belleza de esta definición es que involucra 2 ramas de las matemáticas, la probabilidad y la teoría de los números.

Otras definiciones importantes en el cálculo numérico de π son las que contienen las funciones trigonométricas. Por ejemplo, usando el resultado de $tan\left(\frac{\mathrm{\pi }}{4}\right)=1$ se puede definir $\mathrm{\pi }=4arctan\left(1\right)$. No entraremos en detalle, pero se puede mostrar que con herramientas de cálculo6 y la definición que acabamos de dar que $\mathrm{\pi }=1+\frac{1}{1}+\frac{1}{3}+\frac{1}{5}+\cdots +\frac{1}{(2n+1)}$… Mediante el uso de esta serie, se pueden llegar a precisiones del número π tan grandes como se quiera de forma relativamente rápida con ayuda de computadoras modernas; por ejemplo, hasta noviembre del 2016, el récord en cifras de π era de 22,459,157,718,361 cifras de precisión. El cálculo se puede revisar en: http://www.numberworld.org/y-cruncher/.

Irracionalidad de π

Mejorar la precisión de π llevó a preguntarse si en su expresión decimal no habría una secuencia de números que se repitiera periódicamente como sucede en los números racionales. Por ejemplo, el número 1/3 se puede escribir como 0.33333… repitiendo periódicamente el número 3, o el número 1/7 = 0.142857142857… repitiendo la cadena de cifras “142857” de forma periódica. Si π tuviera una expresión así, sería entonces un número racional, es decir, se podría expresar como una fracción de números enteros (como $\frac{223}{71}$).

La pregunta respecto a la racionalidad de π, fue otro de los grandes problemas en la historia de las matemáticas y tardó algunos siglos en se respondida. En 1761 el matemático francoalemán Johann Lambert (Lambert, 2004), fue el primero en demostrar que el número π no se puede expresar como una fracción, es decir, es irracional. La prueba de Lambert consistió en escribir $tan\left(x\right)$ en la forma: $tan\left(x\right)=a_{0}x+1/(a_{1}x+1/(a_{2}x+1/\left(a_{3}x+..\left)\right)\right)$, donde todos los $a_{\mathit{i}}$ son enteros excepto, quizá, el primero que puede ser una fracción. Finalmente mostrar que si $x$ es un número racional, entonces la fracción tiene una expresión infinita (hay una infinidad de valores de $a_{\mathit{i}}$ diferentes de 0) pero $tan\left(\frac{\mathrm{\pi }}{4}\right)=1$ y 1 es naturalmente una fracción continua finita por ser un entero. Lo que implica que $\frac{\mathrm{\pi }}{4}$ no puede ser un número racional (si lo fuera, la fracción continua no podría ser finita), por lo tanto π tiene que ser irracional.

En general, cualquier número irracional se puede aproximar por números racionales tan bien como queramos. Por eso π se podría aproximar tanto como queramos por una fracción; pero ¿hay alguna forma de medir qué tan bien aproxima un número racional a uno irracional (en particular π)? En 1891, el matemático alemán Adolf Hurwitz (Hurwitz, 1891) demostró que dado un número irracional ψ, existen infinitos números p y q primos relativos (sin divisores comunes) entre sí, de tal forma que: $\left|\begin{array}{cc}\psi & –\frac{p}{q}\end{array}\right|<\frac{1}{\sqrt{5q^2}}$, es decir, el error en la mejor de las aproximaciones es menor que $\frac{1}{\sqrt{5q^2}}$. Por ejemplo, sabemos que 22/7 es una buena aproximación a π puesto que cumple con la desigualdad arriba mencionada, es decir, el error es menor que $\frac{1}{\sqrt{5q^2}}\approx 0.00913$. La desigualdad de Hurwitz, tiene una sola constante, $\sqrt{5}$. Uno podría preguntarse qué sucede si en vez de $\sqrt{5}$ pusiéramos un número más grande, por ejemplo 10 ¿seguiría siendo válida la desigualdad? La respuesta es que para algunos números irracionales esta desigualdad seguirá siendo válida para infinitos valores de q, pero para otros números irracionales no. En particular, para el número dorado $\phi =\frac{(1+\sqrt{5})}{2}\approx 1.618$, la constante más grande que se puede poner es $\sqrt{5}$, pero para otros números irracionales la constante puede ser mayor.

Lo anterior nos lleva a preguntarnos por el grado de irracionalidad de los números, el cual podría medirse calculando el valor de la constante más grande que se puede poner multiplicando a $q$ en la desigualdad de Hurwitz. Entre mayor sea la constante “menos irracional” es el número. Pero se ha descubierto que hay muchos números cuya constante es el infinito. En ese caso, la fórmula de Hurwitz se puede sustituir por $\left|\begin{array}{cc}\psi & –\frac{p}{q}\end{array}\right|<q^{–\alpha }$ con α un número mayor o igual que 2. Se define entonces a α como el grado de irracionalidad de un número. Entre más grande, menos irracional es el número.

El físico y matemático francés Liuville (Wells, 1997) mostró que existen números irracionales (hoy conocidos como números de Liuville) que tienen la propiedad de aproximarse tan rápidamente mediante números racionales que α=∞. Se ha probado que los números algebráicos (los que son solución de una ecuación polinomial, por ejemplo, solución de $6x^5–2x^2+1=3$), son “muy” irracionales, en el sentido de que su grado de irracionalidad es 2, siendo los más irracionales de todos los números.7 Si el número π fuera un número algebraico, sería entonces un número muy irracional.

Volviendo al tema de la cuadratura del círculo, en 1843, el matemático y físico francés Joseph Liuville revisó los manuscritos de Evariste Galois (Liouville, 1846 y Neuenschwander, 1989), quien en 1831 habría escrito, poco antes de morir en un duelo, la demostración sobre la imposibilidad de construir cualquier segmento de longitud que no sea un número algebraico (a estos números se les llama trascendentales). De esta forma, si π fuera algebraico cabría la posibilidad de que se pudiera cuadrar el círculo, y su grado de irracionalidad sería 2, mientras que si fuera trascendental (no algebraico), entonces no se podría cuadrar el círculo (pues si π es trascendental, también lo es $\sqrt{\mathrm{\pi }}$) pero a cambio quedaría abierta la pregunta sobre el grado de irracionalidad de π. En 1882, el matemático alemán Ferdinand Lindermann (Lindermann, 1882) demostró que π es un número no algebraico y con ello se concluyó que no se puede cuadrar el círculo, sin embargo, abrió la posibilidad a que el grado de irracionalidad de π sea mayor a 2.

Medir el grado de irracionalidad de π es importante porque nos podría dar pista sobre cuál es la mejor forma de aproximar este número sin la necesidad de guardar tantas cifras decimales que ocupan mucha memoria. Por otro lado, en 1963 los físicos y matemáticos Kolmogorov, Arnold y Mosel (Arnold, 1963) hicieron una teoría matemática sobre la estabilidad de sistemas no lineales (sistemas dinámicos en el que el cambio en la respuesta del sistema a un estímulo no es proporcional a ese mismo estímulo). Para entender el resultado de estos 3 personajes, vale la pena hacer experimento imaginario. Supongamos que tenemos un péndulo doble como el de la figura 3. Si movemos adecuadamente el péndulo impulsándolo desde abajo, el sistema oscilará tal como oscila un péndulo de un reloj. Sin embargo, si golpeamos (perturbamos) el péndulo de arriba, el movimiento del sistema compuesto pasará a ser caótico (impredecible). Qué tan fuerte tenemos que golpear al péndulo para volverlo caótico depende del grado de irracionalidad de $\raisebox{1ex}{$l_1$}\!\left/ \!\raisebox{-1ex}{$l_2$}\right.$, la razón entre la longitud del primer péndulo y la longitud del segundo. Así, conocer el grado de irracionalidad de un número nos puede dar pista sobre qué tan estables son ciertos sistemas. Puesto que el número π es muy frecuente en la naturaleza, nos interesa saber qué tan irracional es.

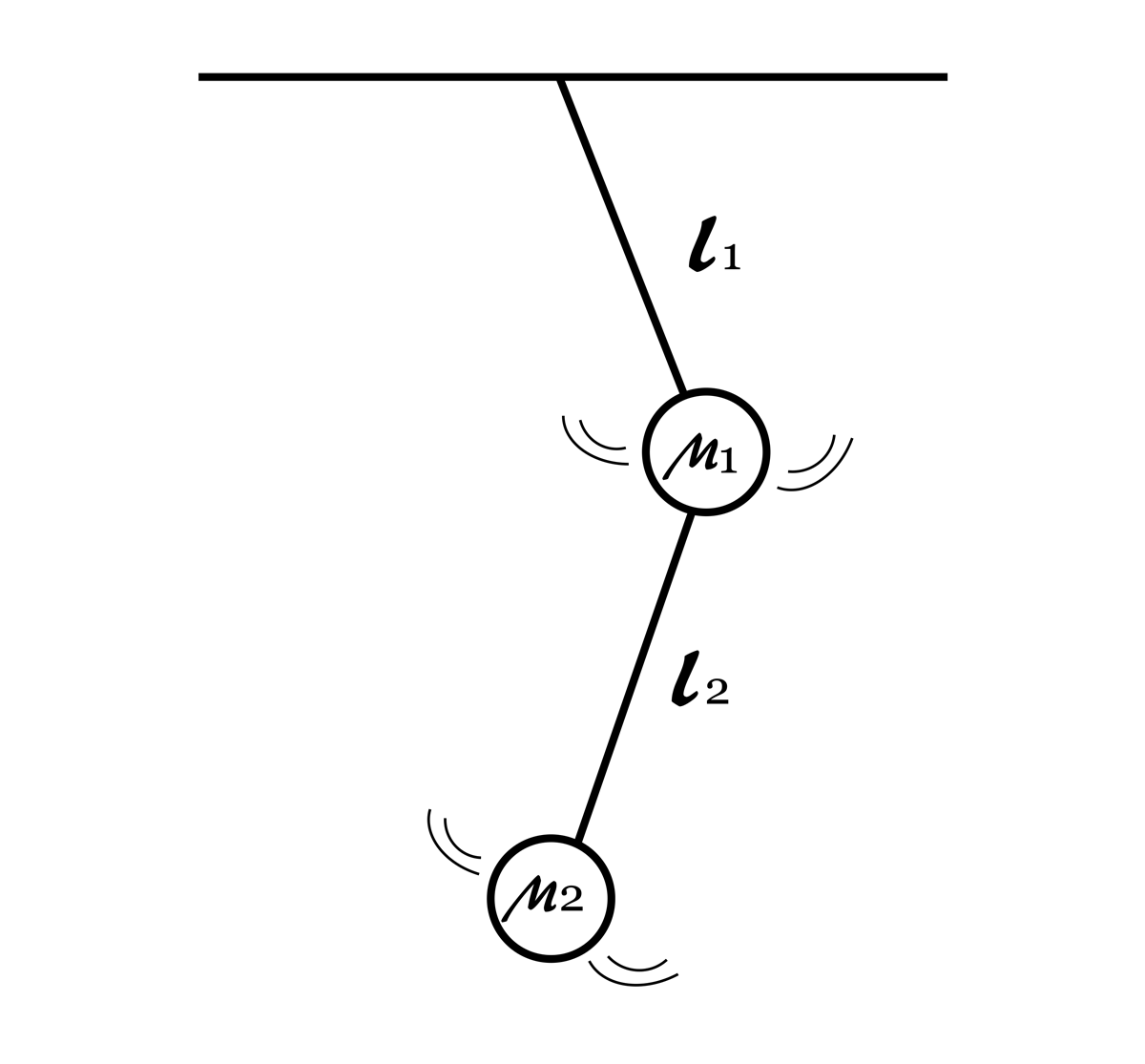
Figura 3. Esquema de un péndulo doble.

Hoy en día se tienen relativamente pocos avances para saber el grado de irracionalidad de π, la mayoría de estos avances son cálculos numéricos; sin embargo, dada la dificultad para medir el exponente, la precisión numérica que se tiene sobre el grado de irracionalidad sigue siendo bastante mala. Analíticamente, Salikhov logró acotar el grado de irracionalidad de π por α$<7.6063$ (Salikhov 2010), sin embargo, las estimaciones numéricas parecen mostrar que este exponente es más bien cercano a 2.

Primer problema abierto: ¿Cuánto vale el grado de irracionalidad de π? En un esfuerzo por mejorar la cota del exponente, Alekseyev (2011) conjeturó que la serie: $\sum _{n=1}^{\infty }\frac{1}{n^3{\sin }^2\left(n\right)}$ es convergente, y con ello logró mostrar que si su conjetura es verdadera, entonces el grado de irracionalidad de π tiene que ser menor que 2.5, lo cual mejora mucho la cota del grado de irracionalidad de π; sin embargo, sigue abierto el problema sobre la convergencia de la serie. Por eso, un problema quizá más sencillo a resolverse es verificar la convergencia de esta serie. Segundo problema abierto: Demostrar que la serie $\sum _{n=1}^{\infty }\frac{1}{n^3{\sin }^2\left(n\right)}$ es o no convergente.

Normalidad de π

Como dijimos previamente, parte del interés en medir el grado de irracionalidad de π es encontrar una forma compacta de aproximar esta constante. Otra forma sería encontrar una estructura en las cifras del desarrollo decimal de π. Por ejemplo, el número 1.234567891011… es un número irracional cuya estructura es bastante clara y, por lo tanto, agregar cifras decimales a su desarrollo resulta sumamente fácil. Por otro lado, resulta fascinante en sí entender la estructura de las cifras en el desarrollo decimal de un número, de alguna forma nos arroja información sobre la naturaleza misma de éste y por lo tanto nos da información sobre la naturaleza de los problemas donde aparece π.

¿Existirá una estructura similar al de 1.234567… en π de forma oculta? Esta pregunta es la que sugiere el cineasta Darren Aronovsky en su película Pi, el orden del caos, donde el protagonista es un matemático que busca secuencias dentro del desarrollo decimal de π. Si no tuviera ninguna estructura, sería entonces un desarrollo desordenado de números, como si se hubiera construido lanzando números al azar. Si este fuera el caso, entonces las cadenas de cifras deberían estar distribuidas de forma homogénea (a veces se dice de forma normal). Cuando un número tiene una distribución homogénea de cifras se dice que el número es normal. Una buena pregunta es entonces si π es un número normal. Si π fuera normal, entonces podríamos usar sus cifras como un generador de números aleatorios.

Tercer problema abierto: ¿Es π un número normal? Sobre este problema realmente no hay muchos avances al respecto, excepto por revisiones numéricas, donde todo parece indicar que las cifras 0-9 aparecen todas con una distribución homogénea (la probabilidad de seleccionar una cifra dada es 1/10). Más aún, se han hecho estudios sobre cadenas de algunas cuantas cifras y hasta ahora pareciera que la probabilidad de tener una cadena de n cifras es $\frac{1}{{10}^n}$ tal como se esperaría si π fuera un número normal; pero de hecho no se sabe ni siquiera si cualquier cadena de números aparece dentro del desarrollo decimal de π.

Esto nos lleva a un problema más sencillo con respecto de la normalidad de π, pero que tampoco se ha resuelto, nuestro cuarto y último misterio sin resolver: Problema abierto 4: ¿Aparecen todas las cadenas de cifras en el desarrollo decimal de π?

Una curiosidad es que existen algunas páginas en internet donde es posible buscar dentro de los primeros cientos (o miles) de cifras de π, una cadena dada, por ejemplo, tu fecha de cumpleaños en el formato: ddmmaaaa, que consta de 8 cifras. En algunos casos se usa la versión corta de fechas dd-mm-aa, donde sólo se usan 6 cifras, es decir, si π es normal, uno de cada millón de cifras contiene tu fecha reducida de cumpleaños aproximadamente.

¿Por qué estudiar π?

Para terminar este texto quiero hacer una reflexión sobre qué importancia tiene conocer si existe cualquier cadena dentro del desarrollo de π. La primera respuesta que podría argumentar es que muchos conocimientos en la ciencia y en particular en las matemáticas han encontrado aplicación decenas o incluso cientos de años después de ser descubiertos y éste podría ser el caso a estos problemas. Por otro lado, hay una estética detrás de π y eso será, para muchos, motivación suficiente para estudiar sus propiedades; después de todo, si disfrutamos entender un proceso, es justificación suficiente para estudiarlo; sin embargo, existen otros motivos para interesarse en las propiedades de π.

Tanto en matemáticas, como en física, π aparece una y otra vez en diversas ecuaciones. En física está presente en las ecuaciones de Maxwell, en el principio de incertidumbre de Heisenberg, en el periodo del péndulo, etcétera. Mientras que en matemáticas está en la probabilidad de que dos números enteros sean primos relativos, en la distribución gaussiana, en desarrollos de Fourier, etcétera. Esto nos dice un poco sobre la importancia que tiene esta constante, por eso, entender sus propiedades es de sumo interés. Al estudiar las propiedades de π de cierta forma logramos comprender que, si hay una función periódica, o hay azar en un proceso, probablemente aparecerá π. De forma inversa, si encontramos π en alguna ecuación o medición, probablemente estará relacionado con una periodicidad o un proceso azaroso. Además, cuando se trata de algo isotrópico, es decir, cuando el comportamiento es el mismo en todas direcciones, aparece nuevamente π por tratarse entonces de algo radial, es decir, sobre una esfera, donde cada capa sigue las mismas reglas. Entender las propiedades de π nos puede llevar a descubrir otra clase de procesos donde la constante podría aparecer. ¿Por qué nos interesamos en π y no otras constantes? Porque sí nos interesamos también en otras constantes, aunque es verdad que hay algunas que son más importantes que otras por la frecuencia con la que las encontramos en la naturaleza, π es una de las más frecuentes y me atrevería a decir que es quizá la más frecuente de las constantes quitando el 0 y el 1.

Este artículo está basado en la plática que dio el autor con el nombre “problemas abiertos acerca de pi” en el marco de la celebración del Día de Pi 2018 organizado por el SUMEN.

Agradecimientos

Agradezco el apoyo de Cedrela Loera tanto con correcciones de estilo, como con las imágenes proporcionadas.

Referencias

• Malisani, E. (1987) Construcción del pentágono regular con sólo compás. Revista de Educación Matemática, 3(2).
• Petrie, W. M. F. (1940). Wisdom of the Egyptians: With 128 Figures (Vol. 63). British school of archaeology in Egypt and B. Quaritch Limited, London, UK. Nota: El libro hace referencia al papiro de Rhind, que se puede consultar en: http://www.britishmuseum.org/research/collection_online/collection_object_details.aspx?objectId=110036&partId=1.
• Lindemann, F. (1882). Über die Zahl π.*. Mathematische Annalen, 20(2), 213-225.
• Goodwin, E. J. (1894). Quadrature of the circle. Amer. Math. Monthly, 1, 246-247.
• Arndt, J., y Haenel, C. (2001). Pi-unleashed. Springer Science & Business Media. p.170.
• Schepler, H. C. (1950). The chronology of pi. Mathematics Magazine, 23(4), 216-228.
• Posamentier, A. S., & Lehmann, I. (2004). Pi: a biography of the world’s most mysterious number. Prometheus Books, New York, NY.
• Lambert, M. (2004). Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques. In Pi: A Source Book (pp. 129-140). Springer, New York, NY.
• Hurwitz, A. (1891). Über die angenäherte Darstellung der Irrationalzahlen durch rationale Brüche. Mathematische Annalen, 39(2), 279-284.
• Wells, D. (1997). The Penguin dictionary of curious and interesting numbers. Penguin. London, UK.
• Liouville, J. (1846). Oeuvres Mathématiques d’Évariste Galois. Journal de Mathématiques pures et appliquées, 11, 381-384.
• Neuenschwander, E. (1989). The unpublished papers of Joseph Liouville in Bordeaux. Historia mathematica, 16(4), 334-342.
• Arnold, V. I. (1963). d, Proof of a theorem of AN Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian, Uspehi Mat. Nauk, 18, 13-40.
• Salikhov, V. K. (2010). On the measure of irrationality of the number π. Mathematical Notes, 88(3), 563-573. Alekseyev, M. A. (2011). On convergence of the Flint Hills series. arXiv preprint arXiv:1104.5100.

Recepción: 02/05/2018. Aprobación: 06/08/2018.