Rigidez y flexibilidad en redes

Consideremos el problema de calcular cuantas barras se requieren para hacer rígido un sistema de N pivotes. Primero debemos saber que caracteriza al sistema cuando éste es rígido. La cuestión es simple: cuando el sistema es rígido, las distancias y los ángulos entre cualesquiera dos pivotes permanecen fijos. 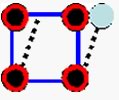En cambio, el sistema tiene partes flexibles si al menos un pivote puede moverse respecto a los otros. La figura muestra un ejemplo simple en dos dimensiones: 4 pivotes unidos por 4 barras.

Cuadrado Flexible. Los pivotes se marcan con círculos, las barras con líneas azules. El cuadrado se puede deformar según las líneas punteadas.

En el caso de la figura anterior, el sistema es flexible, dado que puede deformarse porque los ángulos entre las barras pueden modificarse, según se indica con el cuadrado punteado. Necesitamos introducir una barra en la diagonal para que el cuadrado se vuelva rígido:

Cuadrado isoestático.
No puede deformarse

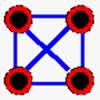En este caso, el sistema tiene el número mínimo de barras necesarias para ser rígido, por lo cual se dice que es isoestático (¿contesta esto porqué los triángulos se prefieren a los cuadrados?). Al introducirse una barra extra, el sistema se vuelve sobrerigidizado, es decir, es rígido pero le sobran barras:

Cuadrado rígido. Sobra una barra, porque el sistema necesita sólo una en la diagonal para que deje de ser flexible.

El ejemplo discutido en el párrafo anterior contiene los elementos básicos de la teoría de la rigidez e ilustra como contando conexiones entre pivotes los sistemas pueden dividirse en tres clases: flexibles, rígidos e isoestáticos. No hemos contestado todavía la pregunta original, pero al menos hemos avanzado en clarificar que debemos estudiar el movimiento relativo entre pivotes. En primera instancia, pueden usarse matemáticas elementales para contestar estas preguntas. Sólo se necesita saber contar.