| |
Cosmos
Agua
Fuego Tierra Aire
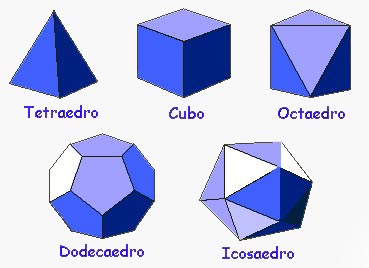
FIG.
4: Sólidos Platónicos. El significado
etéreo dado por los griegos esta para cada
uno de ellos.
De acuerdo a los griegos sólidos daban lugar
al universo.La parte más interesante es que
estas estructuras poseen propiedades diferentes
con respecto a sus contrapartes cristalinas (las
propiedades electrónicas de agregados de
oro son bastante diferentes de las del sistema cristalino,
por ejemplo su color es diferente y depende del
tamaño). Las formas estructurales que pueden
adquirir son muy diversas, pero solo algunas predominan.
Sorprendentemente,
éstas se pueden obtener como extensiones
o realizaciones de los denominados sólidos
platónicos, que se resumen en la figura 4.
Éstos son básicamente poliedros regulares
(un poliedro es un sólido con caras planas).
La parte mas interesante es que estos poliedros
se pueden relacionar al número 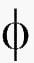 ,
que de nuevo, mágicamente, hace su aparición
en las relaciones de estas formas geométricas. ,
que de nuevo, mágicamente, hace su aparición
en las relaciones de estas formas geométricas.
Por ejemplo, si se toman 3 rectángulos que
siguen la relación del número áureo
(la base es a la altura como el número de
oro) y se intersectan a ángulos de noventa
grados, obtenemos un objeto con 12 esquinas, si
dibujamos en cada esquina un pentágono centrado
en ellos, obtenemos un perfecto dodecaedro, como
el que aparece en la figura 4. Las doce esquinas
también resultan ser las 12 esquinas en las
que se unen los triángulos que forman el
isosaedro (ver figura 4).
En
el caso del poliedro de 120 lados, cada uno de los
vértices se puede obtener como un múltiplo
del número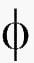 . Dentro de este poliedro de 120 lados, se pueden
circunscribir muchos otros, por lo que también
pueden ser representados a partir del número
. Dentro de este poliedro de 120 lados, se pueden
circunscribir muchos otros, por lo que también
pueden ser representados a partir del número
 .
Esto explica en cierta manera que los sólidos
platónicos contengan muchas de las estructuras
que aparecen a escala nanoscópica y que el
número .
Esto explica en cierta manera que los sólidos
platónicos contengan muchas de las estructuras
que aparecen a escala nanoscópica y que el
número 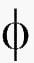 contenga
a todos los sólidos platónicos, dando
una relación universal para entenderlos. contenga
a todos los sólidos platónicos, dando
una relación universal para entenderlos.
 |
Una
de las estructuras más famosas hoy
en día, en el área de nanotecnología,
es el fulereno de 60 átomos de Carbono
(con un diámetro del orden de 7.5 x
10 -10 m), que se puede construir de manera
muy sencilla: considere una pelota de fútbol
que tiene un diámetro del orden de
22 cm, en cada vértice coloque un átomo
de carbono y ahora escale esta forma a que
tenga el diámetro del denominado fulereno.
|
.
Esta estructura también tiene una relación
muy cercana al número ?, ya que las
coordenadas de cada una de las posiciones
de los átomos se puede obtener como
múltiplos del número ?. Esta
forma estructural de carbonos bastante estable
tanto mecánicamente como electrónicamente.
Es entonces de esperar que estructuras obtenidas
bajo transformaciones en las que el número
de oro aparece también se comporten
de la misma manera? |
 |
figuras
geométricas (imágenes)
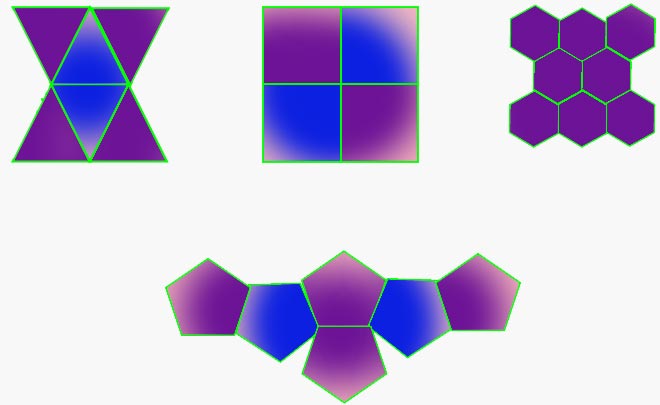
FIG.
5: Uso de diferentes simetrías para el llenado
de una superficie plana. Observe que la simetría
5, tiene vacíos que no puede llenar.
|
|