| |
Afinidad
del 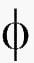 con
respecto a la geometría y la ciencia de materiales
Fig.5
|
Otro ejemplo en la física, donde estas
relaciones aparecen de manera muy clara, es
en las denominadas losetas de Penrose. El
problema se propone de la siguiente manera:
¿Cómo podemos cubrir un espacio
bidimensional usando sólo figuras geométricas
de una cierta simetría? Hasta no hace
muy poco se creía que solamente se
podía hacer con formas de cierta simetría
como se muestra en la figura 5. El
caso de simetría cinco, es decir, con
pentágonos. A primera vista uno decidiría
que no se puede llenar un espacio bidimensional
con esta forma. Recuerde que el número
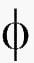está
asociado al pentágono en sí.
Fue en los 70's cuando el matemático
Roger Penrose propuso una manera de poder
hacerlo. Básicamente él encontró
que la superficie se podía cubrir con
formas geométricas basadas en el número
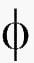que se conocen como losetas de Penrose y como
se muestra en la Fig. 6
|
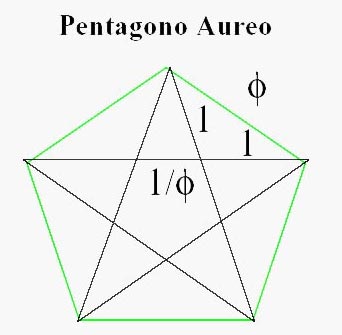
Fig.6
|
Una
realización del recubrimiento espacial
se muestra en la misma figura. Independientemente
de cual de las losetas se use, al final se
puede probar que para poder cubrir correctamente
el espacio, la proporción de losetas
de un tipo con respecto a otro converge de
nuevo al número .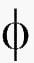
Aunque éste pareciera ser nada más
una curiosidad matemática, resulta
de gran actualidad en la ciencia de materiales,
en los denominados cuasi-cristales, que son
básicamente estructuras que no son
completamente cristalinas y que presentan
manifestaciones como las de sistemas desordenados
(vidrios).
Observados
por primera vez en sistemas de aluminio-manganeso
(Al6Mn), pero desde entonces han sido observados
en muchos otros sistemas tales como: Nb- Fe,
Al-Mg-Zn, Al-Ni-Co, V-Ni-Si, Cr-Ni, etc .
|
FIG.
6: Representación de las losetas de Penrose
que se sacan de partes del pentágono regular
o áureo.
En
la literatura se pueden encontrar muchos otros ejemplos,
que aquí no han sido incluidos, pero esperamos
haber presentado una visión muy rápida
de la importancia del número áureo
y su aparición en la teoría de proporciones.
Ninguno de los ejemplos que discutimos aquí
es la representación de la perfección,
pero si resulta fascinante que exista una tendencia
natural que aparece muy frecuentemente y que no
podemos explicar en base a un evento únicamente
aleatorio. Sólo queremos hacer hincapié
que así como nosotros tratamos de manipular
y modificar la naturaleza a nuestro antojo, ella
también se ha tomado el tiempo de desarrollar
leyes que, aunque lejos de nuestra comprensión,
aparecen de manera repetitiva en muchos de sus eventos.
Agradecimientos
EL
autor agradece a sus colaboradores, Prof. Cristian
Mourkarzel del CINVESTAV, Unidad Mérida,
Dr. Jorge Serrano, Dr. José Luis Rodríguez
por sus comentarios agudos y acertados durante la
lectura de este artículo. Un especial agradecimiento
a Tatiana y a mi hija quienes me recuerdan día
a día que la naturaleza esta llena de sorpresas.
El autor también agradece el apoyo recibido
por el proyecto de la Universidad de California.
Losetas
de Penrose
Pentágono Áureo
FIG.
6:La figura de abajo representa una realización
del recubrimiento en dos dimensiones usando las
losetas y que ha sido tomada de la pagina
http://www.physics.emory.edu/ weeks/pics/qvote3.html
México y los Estados Unidos (UC MEXUS)
y al proyecto CONACYT México J42647-F.
|
|
