Un poco de geometría

En gran medida, si la filosofía de Kant sigue presente en nuestros días, ello se debe a dos factores: por una parte, a las cuestiones que toca; por la otra, a las respuestas que ofrece. Se puede estar en desacuerdo con él; lo que no se puede hacer es dejar sin respuesta las preguntas que elabora. Para hacer comprensible la discusión subsiguiente, hagamos un pequeño recuento de algunas ideas de Kant con relación a las matemáticas. Comencemos con un comentario global.

Kant ve en las proposiciones matemáticas verdades necesarias. No obstante, a diferencia de Leibniz, no ve en ellas proposiciones analíticas, es decir, proposiciones en las que el concepto del predicado P está contenido (implícitamente) en el concepto del sujeto S. En su opinión, las proposiciones matemáticas no se siguen necesariamente del análisis de los conceptos que figuran en ellas; son, por decirlo con sus propias palabras, juicios sintéticos a priori. Al respecto, su preocupación en la Critica de la razón pura no es discutir esta tesis, sino explicar cómo es que son posibles tales juicios. Este es uno de los objetivos de la Estética Trascendental, sección con que Kant abre dicha obra.

Lo que explica la necesidad de las proposiciones sintéticas a priori de la matemática pura es, según Kant, la relación que guardan con las intuiciones puras o a priori del tiempo y el espacio. Tales proposiciones no son juicios empíricos o de experiencia, ni se deducen de ellos. Más bien, las intuiciones que las originan se hallan en nosotros a priori, es decir, con anterioridad a toda percepción de objetos y como una condición de posibilidad de tales percepciones. Al mismo tiempo, lo que distingue al conocimiento matemático de cualquier otra forma de conocimiento a priori es que procede no mediante el análisis de conceptos, sino mediante la construcción de conceptos en el tiempo y en el espacio.

Este es un punto ampliamente debatido en la literatura, del cuál sólo tocaremos algunos aspectos. Comencemos por aclarar en qué estriba la referida "construcción de conceptos". Ésta, en palabras de Kant, consiste en "presentar la intuición a priori que le corresponde [al concepto]". En A 713 y B 741, Kant da claras indicaciones de cómo se debe entender esta caracterización. Veamos su punto de vista a través de un ejemplo tomado de la geometría.

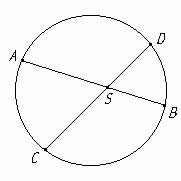
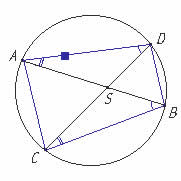
Supongamos que se le pregunta a un geómetra (del siglo XVIII en este caso) acerca de la relación entre los segmentos de cuerdas que se cortan en el interior de un círculo. Por ejemplo, ¿habrá alguna relación entre el producto de sus longitudes? Tratándose de un geómetra, lo primero que hará será trazar (en el papel o en su imaginación) un círculo, tal como nosotros lo hacemos en la figura 1, construyendo a la vez dos cuerdas AB y CD —cuyo punto de intersección es S— como las mencionadas en el enunciado del problema. Después, trazará algunas líneas auxiliares como, por ejemplo, los segmentos AC, AD, BC y BD de la figura 2. Estos elementos lo guiarán en su razonamiento.

SIguiente