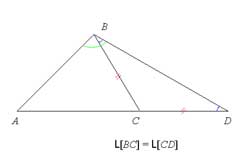
Igualdad de dos figuras

A fin de analizar con mayor cuidado esta visión sobre las proposiciones geométricas podemos partir de aquellas que establecen la igualdad de dos figuras, nos referimos a las proposiciones que aseguran bajo ciertas condiciones la igualdad de dos triángulos, de dos polígonos o dos círculos. Podemos apreciar primero que en todas ellas la igualdad se deriva, directa o indirectamente, de su coincidencia cuando una de las figuras se aplica sobre la otra. Kant asegura que una proposición que establece de esta manera la igualdad puede ser considerada como una proposición sintética que reposa sobre la intuición inmediata y a priori, pues de otro modo no podría tener el carácter de ser apodícticamente cierta y se trataría únicamente de una proposición empírica.

Todas las demostraciones de la igualdad plena (durchgängiger Gleichheit) de dos figuras dadas (de modo que todas las partes de una pueden ser colocadas en el lugar ocupado por las de la otra) se reduce a su coincidencia mutua (sie einander decken); lo cual no es sino una proposición sintética que se apoya sobre la intuición inmediata (unmittelbaren Anschauung); y esta intuición debe ser dada de manera pura y a priori, pues de otro modo esta proposición no podría ser tomada como una proposición apodícticamente cierta y sólo tendría una certeza empírica⁷.

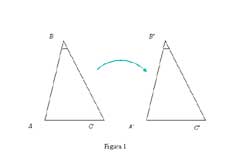
Podemos tomar como ejemplo característico de esta proposición el primer teorema del texto de los Elementos de Euclides, el teorema que asegura la igualdad de dos triángulos cuando dos lados y el ángulo que forman en el primer triángulo son iguales a dos lados y el ángulo que forman en el segundo triángulo. Sabemos que la demostración de Euclides consiste simplemente en hacer ver que los dos triángulos coinciden cuando uno de ellos se superpone al otro.

Figura 1	Figura 2

regresar