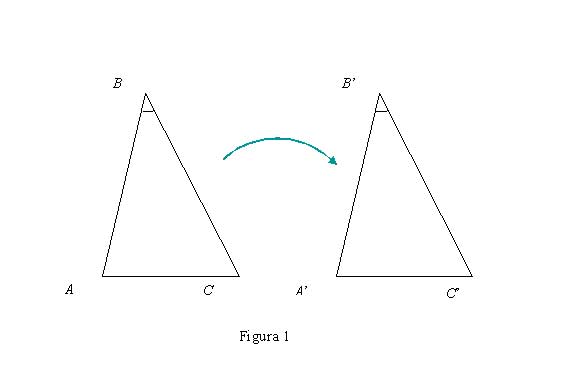
En esta proposición se tiene que con base en la hipótesis de que el lado L[AB] es igual al lado L[A’B’], el lado L[BC] es igual al lado L[B’C’] y el ángulo ?(ABC) es igual al ángulo ?(A’B’C’), se puede concluir que los dos triángulos T[ABC] y T[A’B’C’] son iguales. Como lo señalamos anteriormente, en el texto de Euclides la demostración consiste simplemente en hacer ver la coincidencia de las dos figuras cuando una de ellas se superpone a la otra. Ciertamente podemos asegurar, siguiendo a Kant, que no se trata tan sólo de una proposición cuya certeza dependa simplemente de una experiencia particular (las que deriva de los triángulos aquí presentados) sino que ella descansa sobre una construcción que tiene un carácter a priori y es por lo tanto necesariamente sintética. Podemos asegurar por lo tanto, lo que constituye el núcleo de esta proposición, que si bien en el concepto de triángulo se encuentra contenida la condición de que cualesquiera dos de sus lados forman un ángulo, no es posible derivar analíticamente de ello que el triángulo está determinado de manera única, en forma y magnitud, a partir de dos de sus lados y del ángulo que ellos forman.

Pero a partir de esta primera proposición que establece la igualdad entre dos figuras, se plantea necesariamente la pregunta acerca de si en el caso de la geometría del espacio tridimensional puede darse la misma condición. La proposición que establece la relación entre dos figuras que son perfectamente idénticas en cada una de sus partes, sin ninguna diferencia interna, pero que no se pueden encerrar en los mismos límites y que por lo tanto no coinciden cuando una de ellas se aplica sobre la otra, como es el caso de las dos manos ya mencionado por Kant, tiene igualmente el carácter de ser una proposición sintética. La imposibilidad de que el entendimiento pueda dar cuenta de la diferencia interna que impide la congruencia entre los dos objetos, a pesar de la coincidencia en cada una de sus partes internas, es para Kant la prueba clara de que esta propiedad sólo puede ser explicada en el ámbito de la intuición mediante sus relaciones externas en el espacio. Los objetos incongruentes se presentan como intuiciones sensibles, es decir como apariencias, y es bajo esta condición que adquieren ese carácter: no son representaciones de objetos tal y como éstos son en sí mismos y tal y como el entendimiento los podría conocer. La determinación interna de una región del espacio –la región ocupada por la figura– sólo es posible a través de la determinación de su relación externa con todo el espacio –del que ella es una parte–, pero esta doble determinación sólo es posible a su vez a través de la sensibilidad, ya que el espacio es la forma de la intuición externa de la sensibilidad. A través del entendimiento, en cambio, no es posible dar cuenta de la relación de dos figuras simétricas y no congruentes:

…Ningún concepto es capaz por sí mismo de permitirnos concebir la diferencia entre dos cosas que a pesar de ser semejantes e iguales resultan no congruentes esto sólo podrá hacerse a través de las relaciones que proceden de la intuición⁸.

De este modo Kant señala que tanto en el caso de la igualdad de las figuras planas, como la de desigualdad cuando se trata de figuras sólidas simétricas, es la construcción en la intuición del espacio la que sostiene necesariamente la validez de la proposición. Es ella quien aparece como el sustento del carácter sintético y a priori de la proposición que permite establecer la relación que guardan entre sí las dos figuras.

Un caso similar se tiene con la proposición que asegura que en un triángulo dos lados siempre son mayores que el tercero, la cual adquiere su carácter apodíctico, afirma Kant, del hecho de que ella no se deriva únicamente de un concepto general (el de triángulo) sino de una intuición a priori en la que este concepto es puesto. Se trata en este caso de otra conocida proposición de los Elementos y la demostración que proporciona el texto euclidiano permite nuevamente corroborar su carácter sintético y a priori.