La realidad de los entes matemáticos

Resumen

Esta reflexión es un ejercicio epistemológico que intenta describir el proceso de objetivación de las matemáticas como uno de los muchos modos humanos de objetivar, conocer y construir mundo. Es también una invitación a no cerrar nuestra capacidad cognitiva y a mantenerla abierta a nuevas objetivaciones posibles y construcciones de realidad.
Palabras clave: objetivar, conocer, realidad, matemáticas, números, cantidad.

The reality of mathematical entities

Abstract

This reflection is an epistemological exercise that attempts to describe the process of objectifying mathematics as one of the many human ways of objectifying, knowing and constructing the world. It is also an invitation not to close our cognitive ability and to keep it open to new possible objectifications and constructions of reality.
Keywords: Objectifying, knowing, reality, mathematics, numbers, quantity.

Introducción

El “objeto” de las ciencias no existe como tal, lo que existe para el ser humano es el bombardeo sensorial continuo y dinámico de una realidad1 confusa, maleable, que se nos impone y nos atrapa inevitablemente, pero que también nos seduce, eclosiona a nuestro alrededor y en nosotros mismos, que nos hunde y nos eleva, que nos arrebata y nos estruja, que nos maravilla y desespera.

“Realidad” es una palabra de origen latino cuya traducción al español bien podría ser “coseidad” (la expresión de “cosa” en abstracto), pero una coseidad en la que todo es uno y en la que estamos inmersos hasta la médula, muy a pesar de nuestra inteligencia racionalizante y de su tendencia permanente a objetivar, es decir, a poner distancia, a poner frente a “uno” lo “otro”, como si “uno” no fuera lo “otro” y como si lo “otro” no estuviera de alguna manera en “uno”. Dicho en otras palabras, como si en verdad hubiera algo “otro” y algo “uno” separados.

Cuando no es así, uno mismo es un flujo constante e interminable –mientras vivimos– de pensamientos, sensaciones, sentimientos, sueños y fantasías. Uno mismo sólo se puede denominar “uno” y “yo” con el esfuerzo enorme de retenerse y compactarse en la memoria y objetivarse en la autoconciencia. Esfuerzo en el que se juega nuestra misma racionalidad y lucidez; debido a lo cual, en sus altares quemamos las fantasías “disparatadas”, las locuras no funcionales (o tal vez funcionales, pero en mundos alternos), lo sueños del inconsciente y las preguntas de los niños. Y también limitamos con leyes y costumbres a nuestra libertad, siempre peligrosa y vista bajo la lupa de la sospecha (por ser nuestra apertura a lo posible y, por lo mismo, a lo nuevo).

Este universo del que somos parte, especialmente el universo humano, nos modula y en él nos moldeamos juntos, desde pequeños, a tal grado que –con el paso de los años– olvidamos nuestros sentires primarios y reducimos nuestro sentir a lo ya sentido, lo encajonamos en las reminiscencias de lo ya vivido y aprendido; percibimos lo que nos enseñaron a percibir, y actuamos como nos enseñaron a actuar y, o nos volvemos parte del grupo que sanciona, o seremos sancionados, lo cual puede significar –en muchos casos– la expulsión, la segregación, las etiquetas descalificadoras, el ostracismo. Uno se puede convertir en el extraño al que se tiene que tolerar o el chivo expiatorio al que se debe condenar.

Lo interesante de todo esto es que el que no se asombra con una sensibilidad abierta, el que no pregunta lo que no entiende o no sabe –a pesar de lo obvia que pueda parecer la pregunta–, el que no se lanza a la aventura de la libertad, no sólo se cierra y se va endureciendo, sino que también hace lo mismo con esa realidad con la que se es uno y de la que se está falsamente escindido. También encerramos de manera determinista a lo “otro” y a los “otros”: a todo lo que nos rodea, a nuestra familia, a nuestra sociedad, a nuestro mundo, al universo entero. Afortunadamente, la dinamicidad de la realidad misma no permite que la fosilización sea completa, siempre hay explosiones, resistencias y mutaciones, y siempre necesitaremos viejas preguntas para lo nuevo y nuevas respuestas para lo viejo y, por lo mismo, nuevos tanteos de la libertad liberada de trabas y caminos ya hechos, nuevas caídas y nuevos comienzos.

Así, precisamente así, es como nace y sigue naciendo la ciencia, porque podemos separarnos de la realidad de la que somos parte y podemos dividir a su vez esa misma realidad en millares, millones de “objetos”. Los que a su vez fragmentamos cada vez más para una mejor comprensión y luego nos volvemos locos por volver a unir, porque el costo de la profundización en segmentos cada vez más fraccionados de la realidad, es, en última instancia, el de perder de vista la totalidad y, parafraseando a Salvador de Madariaga (Yuste y Rivas-Caballero, 2016, tercera parte), el peligro de saber cada vez más, acerca de menos. Así que ahora volteamos a nuestro alrededor en busca de otros supuestos “yoes”, que con su mucha profundización en su “objeto propio” nos ayuden a recomponer el rompecabezas en que hemos convertido a la realidad, para, entre todos, recuperar un poco de la unidad perdida en la torre de Babel en que se ha convertido la especialización, y comprender mejor, desde un panorama más amplio que el de la propia mirada fija en un solo punto.

De alguna manera, se trata de un proceso dialéctico, en el que el en sí de la especialidad propia, tiene que confrontarse al fuera de sí de otras especialidades para desalinearlos todos –los en síes y los para síes, los “objetos” y los “sujetos”–, y alcanzar una cierta síntesis en la que lo que se pierdan sean las fronteras, antes infranqueables, de los “objetos” y los egos del especialista; y lo que se gane sea el conocimiento dialógico especializado, pero no cerrado a lo diferente, sino abierto y en reunificación continua.

Detengámonos a reflexionar por un momento en esos primeros procesos de distanciamiento que han dado origen a nuestras ciencias y a los modos que tenemos de comprenderlas y, por lo tanto, de vivirlas; porque volver sobre nuestros pasos hacia atrás puede ayudarnos a desmitificar lo que, sin mucho cuestionamiento, damos por hecho respecto a ellas.

Esta reflexión se centrará entonces en la “reina de las ciencias”, ni más ni menos que en las muy antiguas y respetables matemáticas. Tan respetables, que muchas otras ciencias se apresuran a ponerse en los primeros lugares muy cerca de ellas, tan sólo porque se expresan en su lenguaje. Y otro montón de ciencias de las denominadas sociales y de las humanidades, han hecho esfuerzos valerosos por asumirse como científicas tan sólo porque intentan, o utilizan un lenguaje matemático y métodos cuantitativos para su análisis de datos.

El objeto de las matemáticas

Desde luego que los números no se encuentran dentro de la calculadora, ese aparato no podría tener números si nosotros no lo hubiéramos determinado así. De hecho, aún la numeración que usamos es una construcción y una elección. Los antiguos griegos formaban sus números con puntos, los romanos con letras; pero fueron los números arábigos (cuya función posicional parece que los árabes tomaron de los indios, junto con el uso del cero) los que resultaron más prácticos para, con una nomenclatura sencilla, trabajar y calcular todo lo que se puede “decir” numéricamente hablando: del 0 al 9 tenemos todo lo que necesitamos para expresar cualquier cantidad.

Y he ahí la cuestión, los números son un lenguaje para expresarnos, por eso tantas ciencias pueden recurrir a ellos y tantas otras lo intentan (aunque las particularidades más específicas de los objetos de estudio de ciertas ciencias no sean precisamente expresables en términos matemáticos). Pero los números no son el objeto de las matemáticas, el objeto de las matemáticas es una abstracción, en ella abstraemos por ejemplo la cantidad: lo cuanto.2

¡Qué maravilla! Tenemos la capacidad de abstraer de la realidad la cantidad y solamente la cantidad. Los matemáticos de profesión son una especie de cernidor, que anda por ahí separando las pepitas de oro del lodazal. Para ellos las pepitas de oro son todo lo cuanto, lo cuantificable del universo, y el lodazal que queda es nada más y nada menos que el resto de lo real.

Y la metáfora no es tan equívoca como pareciera, en un lodazal todo parece indiscernible, y sin embargo los gambusinos lograron sustraer oro, y los biólogos seguro encontrarán otras cosas, y los químicos otras, y los niños jugando a las “cocinitas” ¡ni se diga! Todos tenemos la capacidad de objetivar, de distanciarnos, de apreciar sólo uno o unos pocos aspectos del lodazal de lo real, para seguir con la misma metáfora.

Ahora, entremos a la cabeza del matemático: la cantidad no huele, no se ve (su expresión sí, ya lo hemos dicho, pero la expresión no es la cantidad, sino su vehículo), no tiene textura, ni temperatura, no sabe a nada, no hace ruido; en otras palabras, es en extremo abstracta, casi inasible. Por eso, en buena medida, la dificultad que nos presentan las matemáticas a la mayoría de los mortales más acostumbrados a andar por la vida olfateando el viento, escuchando una canción o imaginando animales en las nubes.

La cantidad sólo puede tener medida, y si involucramos a la cantidad en el espacio, entonces, la cantidad se configura y tenemos la geometría. Pero la cantidad es un juguete muy divertido, se puede sumar, restar, multiplicar, dividir, “quebrar”, calcular, y un largo etcétera ad infinitum, porque las ciencias exactas también trabajan con el infinito. Desde la ausencia de cantidad, denominada con aquella expresión con la que solemos comparar a muchos burócratas: “un cero a la izquierda”; hasta la cantidad con la que muchos han equiparado al no cuanto por excelencia: Dios, el Infinito, el Aleph.

La cantidad también se puede exprimir y así expresar lo aparentemente inexistente en el lodazal de lo real, como los números negativos. O puede ser irracional y llevarnos a números que, por facilidad, en algunos casos, expresamos con letras griegas como π ο φ, ya que, por contener infinitos decimales, nunca acabaremos de expresarlos en notación arábiga. Y la cantidad en el espacio nos lleva a figuras maravillosas, perfectas, tan perfectas que no tienen parangón con lo real que conocemos en la cotidianidad, aunque eso real se les parezca un poco: el círculo, el triángulo o el icosaedro, por eso “debemos ser cuidadosos en distinguir las entidades matemáticas precisas de las aproximaciones que vemos a nuestro alrededor en el mundo de los objetos físicos” (Penrose, 2014, p. 53).

Pero… ¿no hemos abstraído la cantidad de lo real cotidiano, de esos objetos físicos a los que ahora debemos aplicar lo abstraído con cuidado? Pareciera que en eso que hemos denominado “realidad” sólo hay dos clases de “cuantos cuantificables” –valga la redundancia– los continuos y los discretos. Los continuos –como el tiempo y el espacio– son indiscernibles en lo que a medida se refiere, y, por eso, nosotros los fragmentamos y medimos arbitrariamente y con medidas externas que nos inventamos. Por ejemplo, al tiempo lo segmentamos en fracciones y hablamos de 1 hora y 46 minutos, o al espacio lo medimos para construir algo y especificamos que lo requerimos de 2 metros y 3.52 centímetros.

En cambio, los cuantos discretos son en general unidades agrupadas que se pueden fragmentar, pero cuya cantidad y peso están ahí en ellas, aunque nosotros nos inventemos los números para expresarlas como cuando decimos el peso de un cuerpo sólido en kilogramos.

Pero, entonces, vuelvo a mi pregunta, pero la reformulo: si las matemáticas son una abstracción que nosotros hemos hecho de lo cuanto (en este artículo nos centramos en lo cuantitativo de las matemáticas), de la cantidad de aquellas cosas a las que denominamos “reales” como, por ejemplo, las vacas, los árboles, las construcciones arquitectónicas y el agua, ¿por qué terminan las matemáticas trabajando con figuras perfectas, con cantidades infinitas, con números negativos y con otras muchas cosas que no encontramos como tal en la realidad cotidiana? Y agrego una pregunta más, ¿por qué las ciencias exactas resultan ser tan sólo probables y aproximativas al medir la cantidad de lo “real” (nuestro mundo cotidiano: las vacas, los árboles, el agua, los puentes, los grupos sociales)? ¿No hay algo aquí que no cuadra?

Y aprovechando que ya estamos metidos en el filosofar, vayamos más lejos aún, ¿no son reales también los números, las figuras perfectas y los números irracionales aun cuando no los percibimos igual que a las aves y las estrellas? ¡Desde luego que sí! Porque, volviendo al inicio de nuestra reflexión, nosotros no somos un “uno” separado de lo “otro”, lo que denominamos “otro” está también en nosotros y tiene muchas maneras de habitarnos, al igual que nosotros en nuestra supuesta “unicidad” habitamos todos los mundos posibles, todos los “objetos” que recortamos y abstraemos de aquella supuesta realidad “otra”. Y como nos habitan y los habitamos, estos objetos abstraídos son realidad, no sólo en nuestras cabezas, sino también en todo lo que nos rodea. La cuestión es que se pueden hacer muchos matices en eso que denominamos “realidad”, las ideas abstractas son también realidades y cuando las utilizamos para comprender y transformar lo natural cotidiano, como una piedra o un trozo de madera, la realidad de lo abstracto termina imponiéndose a la realidad de lo cotidiano de donde fue abstraída. Se impone porque se vuelve una herramienta para transformar esa realidad cotidiana y construir nuevas realidades.

Es así como al detectar una nueva perspectiva de lo real y al abordarla abstrayéndola, esta nueva abstracción nos hace y la hacemos pensar, nos hace y la hacemos hablar, nos hace y la hacemos resonar. Y esa resonancia no es otra cosa que el cultivo lento y paulatino que vamos haciendo con esas semillas “objetuales” –semillas de lo que será “objeto” de estudio, lo que “objetivaremos”–, regadas y abonadas con la sensibilidad y la inteligencia humanas; y eso, cultivado de tantas maneras distintas y a través de las épocas, es lo que denominamos cultura: “el conjunto aprendido de tradiciones y estilos de vida socialmente adquiridos, de los miembros de una sociedad. Incluyendo sus modos pautados y repetitivos de pensar” (Harris, 2011, p.20). Los seres humanos nos cultivamos, nos culturizamos al construir un mundo en común, y construimos este mundo al compartirnos los unos con los otros todo aquello que vamos seccionando de lo que nos rodea para convertirlo en “objeto”, ya sea de estudio, de gozo, de consumo, de uso, o de un largo etcétera.

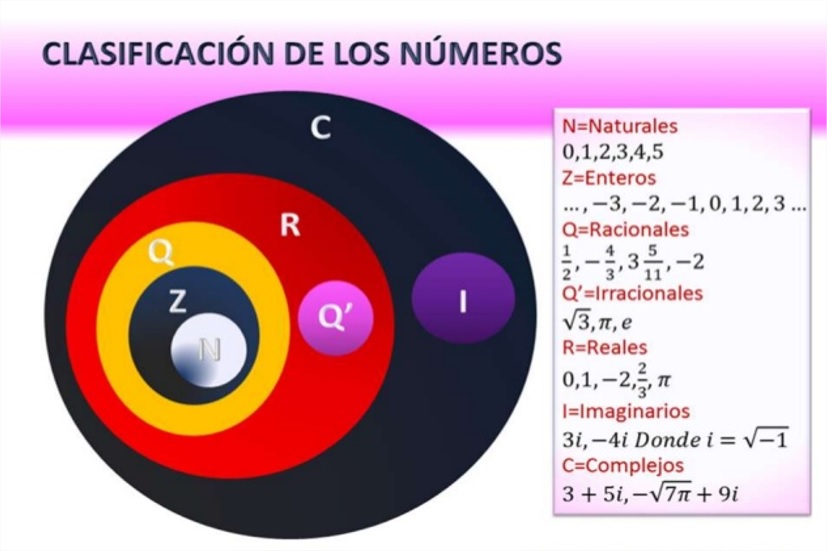
En este sentido, los números son ontológicamente reales; es decir que existen con la misma fuerza de imposición –o tal vez más– que un árbol y forman parte del mundo humano que compartimos. Así, también son reales las figuras geométricas, los axiomas, las fórmulas y los teoremas. Por eso podemos hacer taxonomía de los números y clasificarlos con hermosos diagramas, y hacer ábacos, calculadoras y computadoras; por eso podemos contar, medir, pesar, calcular y sufrir o gozar con las matemáticas; porque sus frutos son reales y tangibles y sus aplicaciones, también. Y así como objetivamos con las matemáticas, también lo hacemos con la química y con la biología, y con las sociedades y con las conductas; y cultivamos y damos frutos. Lo mismo sucede con el arte, con los juegos de los niños y con la comida de la cocinera: sacamos la semilla que es el “objetivar”, seccionando algo de lo que denominamos “real” dentro de nuestra cotidianidad, y lo regresamos después, pero transformado a esa misma realidad de donde lo sacamos. Con eso enriquecemos nuestro entorno y nos enriquecemos y nos ensanchamos nosotros mismos como realidad.

El problema aquí, me parece que no es esa maravilla de las ciencias, las artes y la cultura en general. El problema es que, al objetivar (abstraer, fragmentar de un todo mayor), al ser convertido en notación, en lenguaje, en producto, en un algo aparte de aquello de donde se separó, lo objetivado (ya no se trata de la cantidad de un elefante, ni de la figura de una columna), la cantidad abstracta misma, pasa a formar parte de nuestro entorno como una cosa, como un objeto más de nuestra realidad humana: como número, como medida, como figura geométrica, por ejemplo.

El problema está, entonces, en el olvido de sus orígenes, el olvidar que mucho de lo que nos rodea y de lo que somos no es así a fortiori, sino que así lo hemos hecho nosotros y, por lo mismo, es también cuestionable y transformable. Al olvidar los orígenes del conocimiento que vamos construyendo, en lugar de ampliar, reducimos nuestras posibilidades de crecimiento. En el caso de las matemáticas, “La pregunta ‘La matemática ¿es descubierta o inventada?’ no está bien formulada, porque implica que la respuesta debe ser una o la otra y que ambas posibilidades se excluyen mutuamente” (Livio, Mario, 2011, p. 235), cuando realmente, la respuesta es ambas posibilidades: descubrimos la cantidad, la abstraemos, la procesamos, la pensamos, la reinventamos, la expresamos, y luego aplicamos todo esto que hemos hecho e inventado, con la visibilizada y objetivada cantidad, a todo lo cuanto que nos rodea.

Olvidar la parte creativa de todo esto y dar las cosas por supuestas hace que no se nos ocurra la posibilidad de cuestionarlas, revisarlas y de intentar abrir nuevos caminos, “así, por cierto, puede una racionalidad unilateral, llegar a ser un mal” (Husserl, 1998, p. 113). Somos parte activa de esa realidad fluctuante que nos hace y constituye, pero a la que también nosotros hacemos y constituimos, y prácticamente todo lo que conocemos, lo conocemos ya pensado, digerido y reinventado por los otros que han intervenido activamente en la construcción de mundo.

Si no somos conscientes de nuestra capacidad de objetivar y con esto de actuar para transformar y transformarnos, ni de detectar que las objetivaciones que hacen, en este caso las ciencias, no son cosas en sí ni inamovibles, seremos solamente una parte pasiva de esa fluctuación y, al ser pasivos, seremos también zarandeados, abrumados, y objetivados, digeridos y reinventados por quienes sí trabajan activamente en la constitución del mundo (con independencia de los intereses que los muevan a esto). Así que, ¡busquemos la cuadratura del círculo! Tal vez con otras objetivaciones del espacio esto pierda el carácter de imposibilidad que, de momento, aparenta tener.

Pero, al hacer esto, no debemos olvidar que las objetivaciones ya hechas por la ciencia llevan consigo toda una carga de supuestos: las primeras miradas con las que se han objetivado sus problemas tienden a comprenderse como las únicas maneras posibles de mirar. Las construcciones metodológicas, en muchos casos de exquisita precisión, dependen de esas miradas que se dan por supuestas y ayudan a ver sólo lo que esas miradas nos permiten ver. Los modos de experimentación, de ser el caso, responden también a lo que esas miradas ya supuestas alcanzan a vislumbrar. Los rituales y modelos para informar son fruto de esas visiones oficialmente sancionadas. Por lo mismo, si queremos encontrar la cuadratura del círculo, tendremos tal vez que dejar de mirar por un tiempo, tal vez sea el momento de tantear para aprender a mirar con nuevos ojos, en lugar de sólo mirar para luego tocar solamente lo ya visto.

Imposible objetivar de otro modo las cosas mientras sigamos en el horizonte de las miradas heredadas por siglos de hacer ciencia sólo bajo ciertas perspectivas. ¡Cerremos los ojos! ¡Olfateemos nuestro objeto de estudio! ¡Escuchémoslo también!

Aprendamos a saborearlo con la inteligencia atenta, más que a la respuesta, a la posibilidad de nuevas preguntas. Esto, desde luego, resulta heterodoxo pues es herético dentro de los modos convencionales de hacer ciencia. Pero no existía la ortodoxia, ni la ciencia, antes de las primeras objetivaciones. La ortodoxia se fue construyendo sobre la marcha, y no lo hizo de una manera lineal y sin disrupciones; ni mucho menos, de un modo neutral, como lo percibimos a la distancia dentro de las ciencias ya constituidas.

No se trata de la herejía per se, sino del riesgo que hay que asumir si pretendemos crecer en realidad y en conocimiento, lo que, en última instancia, para el Homo sapiens, viene a ser exactamente lo mismo.

Referencias

• Aristóteles. (2014). Metafísica. Madrid: Gredos.
• Castoriadis, C. (2004). Sujeto y verdad en el mundo histórico-social. México: FCE.
• De Souza santos, B. (2009). Una epistemología del sur. México: FCE.
• García, R. (2000). El conocimiento en construcción. De las formulaciones de Jean Piaget a la teoría de sistemas complejos. Barcelona: Gedisa.
• Harris, M. (2011). Antropología cultural. Madrid: Alianza Editorial.
• Heidegger, M. (2016). Ser y Tiempo. Madrid: Editorial Trotta.
• Husserl, E. (1998). Invitación a la fenomenología. Barcelona: Edición Paidós I.C.E./U.A.B.
• Husserl, E. (2016). Renovación del hombre y la cultura. Cinco ensayos. Barcelona: Anthropos.
• Kuhn, T. (2004). La estructura de las revoluciones científicas. México: FCE. Livio, M. (2011). ¿Es Dios un matemático? Barcelona: Ariel.
• Penrose, R. (2014). El camino a la realidad. Barcelona: Debate.
• Rábade, S. (2010). Teoría del conocimiento. Madrid: Akal.
• Yuste, B. y Rivas-Caballero, S. L. (2016). María Sklodowska Curie. Ella misma. Madrid: Ediciones Palabra.

Recepción: 6/3/2017. Aprobación: 9/8/18.