logo
  Cita PDF
No es lo mismo pero es igual...
José Luis Cisneros Molina
 
Inicio
Busca un artículo
Ejemplares
Vínculos
Nosotros
Convocatoria
Blog
 

 
 
 
Introducción
Relaciones de equivalencia
Clases de equivalencia
Ejemplos de relaciones de...
Relaciones de equivalencia en...
No es lo mismo...

Ejemplos de relaciones de equivalencia en matemáticas

 

En todos nuestros ejemplos, desde la misma definición de la relación de equivalencia podemos ver cuál es el concepto que clasifica a los elementos de $ X$, pero en general no es así, como veremos a continuación.

Veamos algunos ejemplos de relaciones de equivalencia en Matemáticas.

Ejemplo 4   Sea $ \mathbb{N}$ el conjunto de los números naturales:

$\displaystyle \mathbb{N}=\{0,1,2,3,4,5,6,7,8,9,10,11,12,11,12,13,14,15,\dots\}$

y consideremos el conjunto $ \mathbb{N}\times\mathbb{N}$, que consiste de todas las parejas
ordenadas de números naturales

$\displaystyle \mathbb{N}\times\mathbb{N}=\ensuremath{\{\,{(a,b)}\mid {a,b\in\mathbb{N}}\,\}},$

donde ordenadas quiere decir que $ (2,4)$ no es igual a $ (4,2)$.

Sea $ X$ el subconjunto de $ \mathbb{N}\times\mathbb{N}$ de parejas cuyo segundo número es
distinto de cero, es decir

$\displaystyle X=\ensuremath{\{\,{(a,b)\in\mathbb{N}\times\mathbb{N}}\mid {b\neq0}\,\}}.$

Definamos la siguiente relación de equivalencia en $ X$:

$\displaystyle (a,b)\sim (c,d)$   si y sólo si$\displaystyle \qquad ad=bc.$

A primera vista, no es fácil reconocer cual es la propiedad que tienen en común los elementos de una clase de equivalencia (aparte de satisfacer la igualdad anterior). Analicemos por ejemplo la clase de equivalencia de la pareja $ (1,2)$:

$\displaystyle [(1,2)]=\{(1,2),(2,4),(3,6),(4,8),(5,10),(6,12),(7,14),(8,16)\dots\}.$

En este caso, podemos observar que el primer número de la pareja siempre es la mitad del segundo número, por lo que podríamos decir que la propiedad que representa esta clase de equivalencia es la de mitad. Otra manera de ver esto es identificando a cada pareja ordenada $ (a,b)$ con la fracción $ \frac{a}{b}$, entonces podemos ver que todos los elementos de la clase $ [(1,2)]$ representan a la misma fracción:

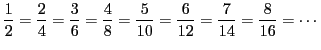
$\displaystyle \frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\frac{6}{12}=\frac{7}{14}=\frac{8}{16}=\cdots$

Por lo tanto, podemos decir que la clase de equivalencia $ [(1,2)]$ es la fracción $ \frac{1}{2}$ y los distintos representantes de la clase, son distintos representantes de la misma fracción.

Ahora, si cada clase de equivalencia $ [(a,b)]$ la estamos identificando con la fracción $ \frac{a}{b}$, entonces el conjunto cociente $ \widetilde{X}$ consiste de todas las fracciones $ \frac{a}{b}$ con $ a$ y $ b$ números naturales y $ b\neq0$. El nuevo concepto con el que la relación de equivalencia $ \sim$ clasifica a los elementos de $ X$ es el concepto de razón entre dos números naturales.

El hecho de que cada fracción tenga muchos representantes distintos es una de las causas de que muchos niños en la primaria tengan problemas para sumar fracciones.

Ejemplo 5   Consideremos nuevamente el conjunto $ \mathbb{N}\times\mathbb{N}=\ensuremath{\{\,{(a,b)}\mid {a,b\in\mathbb{N}}\,\}}$ de parejas ordenadas de números naturales y definamos la siguiente relación de equivalencia en él:

$\displaystyle (a,b)\sim (c,d)$   si y sólo si$\displaystyle \qquad a+d=b+c.$

Analicemos la clase de equivalencia de las parejas $ (2,0),(7,7),(1,2)$:

$\displaystyle [(2,0)]$ $\displaystyle =\{(2,0),(3,1),(4,2),(5,3),(6,4),(7,5),(8,6),(9,7)\dots\},$
$\displaystyle [(7,7)]$ $\displaystyle =\{(0,0),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(7,7)\dots\},$
$\displaystyle [(1,2)]$ $\displaystyle =\{(0,1),(1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8)\dots\}.$

Podemos observar que en los elementos de la clase $ [(2,0)]$ el primer número de la pareja siempre es 2 unidades mayor que el segundo número, en los elementos de la clase $ [(7,7)]$ ambos números siempre son iguales y en los elementos de la clase $ [(1,2)]$ el primer número de la pareja siempre es 1 unidad menor que el segundo número. De manera general, tenemos que en todos los elementos en una clase, la diferencia entre el primer y segundo números es la misma:

$\displaystyle 2-0=3-1=4-2=5-3=6-4=7-5=8-6=9-7=\cdots$
$\displaystyle 0-0=1-1=2-2=3-3=4-4=5-5=6-6=7-7=\cdots$
$\displaystyle 0-1=1-2=2-3=3-4=4-5=5-6=6-7=7-8=\cdots$

Entonces a cada clase de equivalencia la podemos identificar con dicha diferencia, es decir, a la clase $ [(2,0)]$ con el número $ 2$, la clase $ [(7,7)]$ con el número 0 y a la clase $ [(1,2)]$ con el número $ -1$. En general, dada una pareja ordenada cualquiera de números naturales, tenemos tres posibilidades, :

• El primer número es mayor que el segundo. Si $ k,n\in\mathbb{N}$ y $ n>0$, la clase

$\displaystyle [(k+n,k)]$   es identificada con el número positivo $ k+n-k=n$

• El primer número es igual que el segundo. Si $ k\in\mathbb{N}$, la clase

$\displaystyle [(k,k)]$   es identificada con el número $ k-k=0$

• El primer número es menor que el segundo. Si $ k,n\in\mathbb{N}$ y $ n>0$, la clase

$\displaystyle [(k,k+n)]$   es identificada con el número negativo $ k-(k+n)=-n$

Por lo tanto, el conjunto cociente $ \widetilde{\mathbb{N}\times\mathbb{N}}$ se identifica con el conjunto de los números enteros, el cual se acostumbra denotar por la letra $ \mathbb{Z}_{}$, es decir,

$\displaystyle \mathbb{Z}_{}=\{\dots,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,\dots\}$

El nuevo concepto con el que la relación de equivalencia $ \sim$ clasifica a los elementos de $ \mathbb{N}\times\mathbb{N}$ es el concepto de diferencia entre dos números naturales.

Ejemplo 6   Sea $ X=\ensuremath{\{\,{(a,b)\in\mathbb{Z}_{}\times\mathbb{Z}_{}}\mid {b\neq0}\,\}}$ con la misma relación de equivalencia que el Ejemplo 4, es decir:

$\displaystyle (a,b)\sim (c,d)$   si y sólo si$\displaystyle \qquad ad=bc.$

Nuevamente la clase de equivalencia $ [(a,b)]$ puede identificarse con la fracción $ \frac{a}{b}$, pero ahora las fracciones pueden ser negativas. En este caso, el conjunto cociente $ \tilde{X}$ se identifica con el conjunto de los números racionales, el cual se acostumbra denotar por la letra $ \mathbb{Q}$, es decir:

$\displaystyle \mathbb{Q}=\ensuremath{\{\,{\frac{a}{b}}\mid {a,b\in\mathbb{Z}_{},\ b\neq0}\,\}}.$

Ejemplo 7   Sea $ n$ un número entero. Definimos una relación de equivalencia en el conjunto de los números enteros $ \mathbb{Z}_{}$ de la siguiente manera:

$\displaystyle a\sim b$   si y sólo si   $ a-b$ es un múltiplo de $ n$

Esta relación se conoce como congruencia módulo $ n$ y generalmente cuando $ a\sim b$ se denota por $ a\equiv b\mod n$.

Tomemos como ejemplo $ n=5$ y analicemos la clase de equivalencia de $ 1$:

$\displaystyle [1]=\{\dots,-34,-29,-24,-19,-14,-9,-4,1,6,11,16,21,26,31,36,\dots\}$

Despues de observar los números en esta clase de equivalencia no es difícil llegar a la conclusión de que consta de todos los números de la forma $ 5k+1$, donde $ k$ puede ser cualquier número entero. En otras palabras, la clase de equivalencia $ [1]$ consiste de todos los números que al dividirlos entre $ 5$, nos queda como residuo $ 1$. De lo anterior podríamos pensar que:

Una clase de equivalencia consiste de todos los números que al dividirlos entre $ n$ tienen el mismo residuo.

Como en los ejemplos anteriores, podríamos verificar ésto para otras clases de equivalencia, sin embargo, en matemáticas no es suficiente verificar algunos o muchos casos para llegar a una conclusión, lo que hacemos los matemáticos es demostrar que las afirmaciones son válidas en general. Como un ejemplo, daremos una demostración de la conjetura3 anterior.


Demostración. Sea $ b$ un número entero cualquiera y supongamos que al dividir a $ b$ entre $ n$ obtenemos como residuo $ r$, es decir:

$\displaystyle b=kn+r$   para alguna $ k\in\mathbb{Z}_{}$ y $ 0\leq r<n$.          (1)

Lo que queremos demostrar es que todo elemento $ a$ en la clase $ [b]$, al dividirlo entre $ n$ también obtenemos como residuo $ r$.

Como $ a$ está en $ [b]$ tenemos que $ a\equiv b\mod n$, por lo tanto, $ a-b$ es un múltiplo de $ n$, es decir:

$\displaystyle a-b=ln$   para alguna $ l\in\mathbb{Z}_{}$,           (2)

substituyendo (1) en (2) obtenemos:

$\displaystyle a-(kn+r)$ $\displaystyle =ln$    
$\displaystyle a$ $\displaystyle =ln+kn+r$    
$\displaystyle a$ $\displaystyle =(l+k)n+r$    

por lo tanto al dividir a $ a$ entre $ n$ también obtenemos como residuo a $ r$.4


Por lo anterior, el conjunto cociente $ \tilde{\mathbb{Z}_{}}$ de esta relación, que generalmente se denota por $ \mathbb{Z}_{n}$, consiste en las $ n$ clases correspondientes a cada posible residuo $ r$ entre 0 y $ n-1$

$\displaystyle \mathbb{Z}_{n}=\{[0],[1],[2],\dots,[n-1]\}$

y es llamado el conjunto de clases residuales módulo $ n$.

En el caso cuando $ n=2$, tenemos que $ \mathbb{Z}_{2}$ consta de sólo dos clases $ \mathbb{Z}_{2}=\{[0],[1]\}$, la clase $ [0]$ corresponde a los números pares y la clase $ [1]$ corresponde a los números impares.


En los ejemplos anteriores hemos visto que el conjunto de números enteros $ \mathbb{Z}_{}$ y el conjunto de números racionales $ \mathbb{Q}$ pueden verse como el conjunto cociente de alguna relación de equivalencia. El conjunto de números naturales tambien puede verse como un conjunto cociente.

Ejemplo 8   Consideremos a todos los conjuntos finitos y digamos que dos conjuntos están relacionados si podemos encontrar una biyección entre ellos, es decir, si a todo elemento del primer conjunto podemos asociarle uno y sólo un elemento del segundo conjunto y viceversa, por ejemplo

 está relacionado con 

ya que podemos encontrar una5 biyección entre ellos, por ejemplo:

               (3)

Sin embargo

 no está relacionado con  ,

ya que si intentamos encontrar una biyección, siempre saldrá sobrando un elemento del segundo conjunto, por ejemplo:

               (4)

Esta relación es una relación de equivalencia y cada clase de equivalencia consiste de todos los conjuntos con el mismo número de elementos. Por lo tanto, cada clase de equivalencia puede identificarse con un número natural, es decir:

El número $ n$ es la clase de equivalencia de todos los conjuntos que tienen $ n$ elementos.

Así el conjunto cociente se identifica con el conjunto de los números naturales $ \mathbb{N}$. Para una explicación más extensa del concepto de número sugiero leer el texto clásico de Bertrand Russell.


siguiente

subir

siguiente

 



Número actual
Las Matemáticas y su aplicación en comunicaciones digitales
No es lo mismo pero es igual...
Las Matemáticas en nuestro mundo cotidiano
Entrevista:
Las Matemáticas, herramientas invaluables de la vida cotidiana

Biblioteca de Edición Digital

Trayectos
Ecoteca
 
D.R. © Coordinación de Publicaciones Digitales
Dirección General de Servicios de Cómputo Académico-UNAM
Ciudad Universitaria, México D.F.
Se autoriza la reproducción total o parcial de los artículos aquí presentados,
siempre y cuando se cite la fuente completa y su dirección electrónica
 
ndex.htm" />