

| Cita | ||
|---|---|---|
| No es lo mismo pero es igual... | ||
| José Luis Cisneros Molina | ||
|
|
|---|
Relaciones de equivalencia en Matemáticas
En Matemáticas se estudian muchos tipos de objetos, como por ejemplo, conjuntos, grupos, espacios topológicos, por mencionar sólo algunos. Para estudiarlos, se dividen en distintas categorías, las cuales consisten de dos ingredientes: los objetos mismos y de unas cosas llamadas morfismos que sirven para relacionar o comparar a los distintos objetos.
Ejemplo 9.
Consideremos la categoría de conjuntos, en la cual los objetos son
obviamente los conjuntos y los morfismos son las funciones entre
dos conjuntos, las cuales asocian a todo elemento del primer conjunto uno
y sólo un elemento del segundo conjunto. Si ![]() y
y ![]() son dos conjuntos, una función
son dos conjuntos, una función ![]() del conjunto
del conjunto ![]() en el conjunto
en el conjunto ![]() se denota por
se denota por
![]() y si
y si ![]() , entonces
, entonces ![]() denota al elemento de
denota al elemento de ![]() asociado a
asociado a ![]() mediante la función
mediante la función ![]() .
.
Si en (3) consideramos la asignación dada por las flechas que van de izquierda a derecha
![]() tenemos una función del conjunto
tenemos una función del conjunto
![]() en el conjunto
en el conjunto
![]() , con las flechas de derecha a izquierda
, con las flechas de derecha a izquierda
![]() tenemos una función del conjunto
tenemos una función del conjunto
![]() en el conjunto
en el conjunto
![]() . En (4) las flechas
. En (4) las flechas
![]() definen una función del conjunto
definen una función del conjunto
![]() en el conjunto
en el conjunto
![]() , pero las flechas
, pero las flechas
![]() no definen una función del conjunto
no definen una función del conjunto
![]() en el conjunto
en el conjunto
![]() , pues el elemento
, pues el elemento
![]() no tiene asociado ningún elemento del conjunto
no tiene asociado ningún elemento del conjunto
![]() .
.
Ejemplo 10.
Otro ejemplo de categoría es la categoría de grupos,
en la cual los objetos son los grupos. Un grupo es un conjunto ![]() que tiene una operación binaria
que tiene una operación binaria ![]() , es decir, dados dos elementos
, es decir, dados dos elementos ![]() se pueden operar (como sumar o multiplicar) para obtener
otro elemento
se pueden operar (como sumar o multiplicar) para obtener
otro elemento ![]() , lo cual se escribe
, lo cual se escribe
![]() . Además
. Además ![]() tiene un elemento neutro
tiene un elemento neutro ![]() , es decir
, es decir
![]() para todo elemento
para todo elemento ![]() , y todo elemento
, y todo elemento ![]() tiene un elemento inverso
tiene un elemento inverso ![]() es decir
es decir
![]() .
.
Es fácil ver que el conjunto de los números
enteros
![]() con la operación suma +, es un grupo donde
el elemento neutro es el 0 y el elemento inverso del entero
con la operación suma +, es un grupo donde
el elemento neutro es el 0 y el elemento inverso del entero ![]() es
es ![]() . Si al conjunto de los números racionales
. Si al conjunto de los números racionales
![]() (las fracciones positivas y negativas) le quitamos el 0,
entonces con la operación multiplicación x, es un grupo donde
el elemento neutro es el
(las fracciones positivas y negativas) le quitamos el 0,
entonces con la operación multiplicación x, es un grupo donde
el elemento neutro es el ![]() y el elemento inverso de la fracción
y el elemento inverso de la fracción
![]() es
es
![]() . Los números naturales
. Los números naturales
![]() no son un grupo con la operación suma +, pues
no existen los elementos inversos. Otro ejemplo de grupo es
el conjunto
no son un grupo con la operación suma +, pues
no existen los elementos inversos. Otro ejemplo de grupo es
el conjunto ![]() con la operación multiplicación x, donde el elemento
neutro es el
con la operación multiplicación x, donde el elemento
neutro es el ![]() y cada elemento es su propio elemento inverso.
Al final del Ejemplo 7 vimos
que el conjunto
y cada elemento es su propio elemento inverso.
Al final del Ejemplo 7 vimos
que el conjunto
![]() tiene solamente de dos elementos, la clase de equivalencia
tiene solamente de dos elementos, la clase de equivalencia ![]() que consiste de todos los números pares y la clase de equivalencia
que consiste de todos los números pares y la clase de equivalencia ![]() que consiste de todos los números impares. El conjunto
que consiste de todos los números impares. El conjunto
![]() es un grupo con la operación suma
es un grupo con la operación suma ![]() , definida de la siguiente manera:
, definida de la siguiente manera:
la cual refleja que la suma de dos números pares es nuevamente par, la suma de un número par y un número impar es impar y la suma de dos números impares es par. También se observa que ![]() es el elemento neutro y cada elemento es su propio elemento inverso.
es el elemento neutro y cada elemento es su propio elemento inverso.
Los morfismos en la categoría de
grupos se llaman homomorfismos y son funciones que preservan
las operaciones, es decir, si tenemos al grupo ![]() con la operación + y al grupo
con la operación + y al grupo ![]() con la operación
con la operación ![]() , entonces un homomorfismo
, entonces un homomorfismo ![]() del grupo
del grupo ![]() al grupo
al grupo ![]() , es una función
, es una función
![]() del conjunto
del conjunto ![]() en el conjunto
en el conjunto ![]() , tal que si
, tal que si ![]() , entonces
, entonces
![]() .
.
Un ejemplo de un homomorfismo
![]() está definido de la siguiente manera: si
está definido de la siguiente manera: si
![]() es par, entonces
es par, entonces ![]() , si
, si
![]() es impar, entonces
es impar, entonces ![]() . Es fácil ver que si
. Es fácil ver que si
![]() , entonces
, entonces
![]() .
.
En una categoría hay un tipo especial de morfismos llamados isomorfismos, dados dos objetos en la categoría, no necesariamente existe un isomorfismo entre ellos, pero si existe, decimos que dichos objetos son isomorfos6. En una categoría podemos definir una relación de equivalencia definiendo que dos objetos están relacionados si son isomorfos. Las clases de equivalencia consisten de todos los objetos que son isomorfos entre sí, por lo que se les llama clases de isomorfismo. Dichas clases son muy importantes en Matemáticas, pues en una categoría dos objetos isomorfos son considerados como iguales, por lo tanto, al estudiar una categoría dada, uno de los objetivos es encontrar todas las clases de isomorfismo, pues así se conocerán todos los objetos de la categoría que son esencialmente distintos.
Por otra parte, muchas veces dentro de una clase de isomorfismo hay algún objeto que es más simple que todos los demás al cual se le llama objeto reducido y en general es más fácil estudiar al objeto reducido en vez de estudiar cualquier otro objeto isomorfo. También las distintas clases de isomorfismo se pueden representar usando dichos objetos reducidos.
Esto es análogo al Ejemplo 4 donde las clases de equivalencia se podían ver como fracciones, en la clase de equivalencia ![]() la pareja
la pareja ![]() es el elemento más simple, en el sentido de que ambos números son primos relativos entre sí, es decir,
es el elemento más simple, en el sentido de que ambos números son primos relativos entre sí, es decir, ![]() es el único divisor común.
es el único divisor común.
En la categoría de conjuntos los isomorfismos son las biyecciones, (3) es una biyección entre los conjuntos
![]() y
y
![]() y por lo tanto son isomorfos. En general, dos conjuntos son isomorfos si tienen el mismo número de elementos.
y por lo tanto son isomorfos. En general, dos conjuntos son isomorfos si tienen el mismo número de elementos.
En la categoría de grupos los isomorfismos son los homomorfismos que son también biyecciones. Los grupos
![]() y
y ![]() son isomorfos mediante el isomorfismo dado por la siguiente biyección
son isomorfos mediante el isomorfismo dado por la siguiente biyección
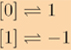
la cual es un homomorfismo pues tenemos que las igualdades
![]()
son exactamente las “mismas” igualdades que en (5),
pero reemplazando ![]() por
por ![]() ,
, ![]() por
por ![]() y + por x. En este ejemplo se puede ver por qué objetos isomorfos (misma
forma) son considerados como iguales, pues vemos que los grupos
y + por x. En este ejemplo se puede ver por qué objetos isomorfos (misma
forma) son considerados como iguales, pues vemos que los grupos
![]() y
y ![]() son prácticamente el mismo, solamente con los nombres
de los elementos y la operación cambiados, o como dice el dicho popular,
son “la misma gata, nada más que revolcada”.
son prácticamente el mismo, solamente con los nombres
de los elementos y la operación cambiados, o como dice el dicho popular,
son “la misma gata, nada más que revolcada”.
En muchas categorías en Matemáticas sus objetos constan de un conjunto con una estructura adicional. Por ejemplo, los grupos son conjuntos y la estructura adicional es la operación binaria. Este tipo de objetos, al ser conjuntos, podemos definir relaciones de equivalencia en ellos y obtener su conjunto cociente, es decir, el conjunto de clases de equivalencia y en general a dicho conjunto cociente se le puede dotar de una estructura adicional para que sea un objeto de la categoría en cuestión, a dicho objeto se le llama objeto cociente. Nuevamente esto se comprende mejor con un ejemplo.
En el Ejemplo 10 vimos
que el conjunto de los números enteros
![]() es un grupo con la operación suma +. En el Ejemplo 7,
definimos la congruencia módulo
es un grupo con la operación suma +. En el Ejemplo 7,
definimos la congruencia módulo ![]() , la cual es una relación de equivalencia en
, la cual es una relación de equivalencia en
![]() y el conjunto cociente es el conjunto
y el conjunto cociente es el conjunto
![]() al cual dotamos de una operación suma +, definida
por (5)
la cual convierte al conjunto
al cual dotamos de una operación suma +, definida
por (5)
la cual convierte al conjunto
![]() en un grupo. Por lo tanto,
en un grupo. Por lo tanto,
![]() es el grupo cociente obtenido por la relación
de equivalencia dada por la congruencia módulo 2.
es el grupo cociente obtenido por la relación
de equivalencia dada por la congruencia módulo 2.
| Número actual |
|---|
| Ecoteca |
Dirección General de Servicios de Cómputo Académico-UNAM
Ciudad Universitaria, México D.F.
Se autoriza la reproducción total o parcial de los artículos aquí presentados,
siempre y cuando se cite la fuente completa y su dirección electrónica


