¿Cómo podemos encontrar la mejor ruta de recolección de basura?

Resumen

Enfrentando el desafío de optimizar la recolección de basura en la colonia Rosarito, Los Cabos, México, utilizamos herramientas de la Teoría de Gráficas para modelar y resolver el problema. Construimos una gráfica que representa la disposición de calles y aplicamos el algoritmo de Fleury, modificado para minimizar vueltas en U. Al no contar con una gráfica euleriana, añadimos aristas para garantizar recorridos completos y utilizamos el algoritmo de Kruskal para obtener un árbol generador de peso mínimo. Los resultados revelan una ruta óptima con una distancia reducida de 0.695 km en comparación con la ruta actual, generando un ahorro anual significativo de aproximadamente 108.718 km. La propuesta elimina vueltas en U evitables, mejora la eficiencia en la recolección y presenta aplicaciones potenciales en otros contextos logísticos urbanos.
Palabras clave: teoría de gráficas, recolección de basura, logística urbana, gestión de residuos, gráfica euleriana.

How can we find the best garbage collection route?

Abstract

Facing the challenge of optimizing garbage collection in the Rosarito neighborhood, Los Cabos, Mexico, we utilized tools from Graph Theory to model and solve the problem. We constructed a graph representing the street layout and applied the Fleury algorithm, modified to minimize U-turns. Without a Eulerian graph, we added edges to ensure complete routes and employed the Kruskal algorithm to obtain a minimum-weight spanning tree. Results reveal an optimal route with a reduced distance of 0.695 km compared to the current route, leading to a significant annual savings of approximately 108,718 km. The proposal eliminates avoidable U-turns, enhances collection efficiency, and holds potential applications in other urban logistics contexts.
Keywords: graph theory, garbage collection, urban logistics, waste management, Eulerian graph.

El problema de recolección de basura

Imagina que eres chofer de un camión recolector de basura y debes recoger, casa por casa, la basura de una colonia. Te dan el mapa de la colonia. ¿Cómo realizarías el trayecto? ¿Serías capaz de encontrar una ruta que transite por todas las calles recorriendo la menor distancia posible? ¿Sabes que algunos algoritmos matemáticos podrían ayudarte a encontrar tal ruta?

El objetivo es que, además de pasar por todas las casas de todas las calles de una colonia, se logre hacerlo ahorrando tiempo, energía y costos de operación. Hay muchas maneras de abordar este problema; en este artículo, lo haremos usando las herramientas de un área muy útil de las Matemáticas: la Teoría de Gráficas.

Sabemos que es de vital importancia que las ciudades cuenten con un sistema de recolección eficaz para tener una ciudad libre de residuos sólidos. Estos son un problema porque podrían ocasionar enfermedades, proliferación de fauna nociva, malos olores y una vista desagradable que impactaría negativamente al turismo, así como a otras actividades económicas y recreativas.

Pensando en esto, nos abocamos a buscar una ruta óptima de recolección de basura en la colonia Rosarito del municipio de Los Cabos, Baja California Sur en México. Cuando decimos óptima, nos referimos a aquella ruta que efectivamente pase por todos los hogares de la colonia y que recorra la menor cantidad de kilómetros, para así ahorrar en combustible, en tiempo y en mantenimiento de la unidad recolectora.

En la siguiente sección presentamos los conceptos matemáticos que usaremos para modelar nuestra propuesta de solución.

Recogiendo la basura de manera eficiente

Como sabes, las Matemáticas son una de las más poderosas creaciones humanas. Nos han dado herramientas útiles para resolver una infinidad de problemas. Su versatilidad nos ha llevado desde el espacio exterior hasta el mundo microscópico. La Teoría de Gráficas ha sido una de las áreas más interesantes y versátiles para resolver problemas cotidianos como el de la recolección de basura. Nuestra propuesta de solución modela el problema usando gráficas y algoritmos.

Pero ¿qué es una gráfica? Aquí es necesario introducir algunas definiciones. Una gráfica es una colección de puntos (vértices) y líneas (aristas) que unen a parejas de ellos. Se coloca una arista cuando dos vértices están relacionados. Entonces, las gráficas sirven para representar relaciones entre objetos —o personas u otros elementos—. Por ejemplo, si hay un grupo de cinco personas, podemos representar a cada persona con un vértice y colocar una arista entre dos personas que tengan la misma edad (en años cumplidos). ¿Cómo quedaría la gráfica si las cinco personas tienen la misma edad? La Figura 1 muestra la gráfica que modela este ejemplo.

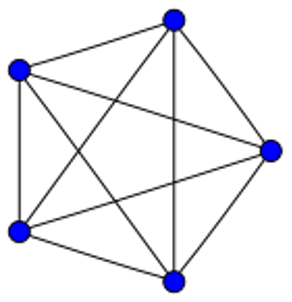
Figura 1. Gráfica que representa a 5 personas con la misma edad. Crédito: elaboración propia.

Así de fáciles son las gráficas. Siempre que haya una colección de objetos y una relación entre ellos, podemos dibujar una gráfica —en este ejemplo son personas, pero podrían ser cosas, empresas, escuelas o lo que se te ocurra—. Las gráficas pueden ser muy lindas e interesantes al mismo tiempo y por esto mucha gente se ha dedicado a estudiarlas, no solamente para resolver problemas cotidianos, sino además para entender sus propiedades (Chartrand et al., 1996).

Existen un sinfín de gráficas que modelan o que se construyen para estudiarlas. Un par de ejemplos son los mostrados en la Figura 2, que destacan por su belleza.

Figura 2. Otros ejemplos de gráficas. Crédito: elaboración propia.

Problemas de recorribilidad

La Teoría de Gráficas modela y resuelve, entre muchas situaciones, los problemas de recorribilidad, que son aquellos en los que hay que localizar rutas óptimas en una zona o región determinada. Lo que se hace es modelar la zona mediante una gráfica, buscar y construir el recorrido en la gráfica, para después realizarlo en la zona real. De hecho, esta área de las Matemáticas surgió precisamente al resolver uno de estos problemas.1

En la siguiente sección, explicaremos cómo usamos la Teoría de Gráficas para modelar y resolver el problema de recolección de basura en la colonia Rosarito en Los Cabos, Baja California Sur, México.

La propuesta

Iniciamos construyendo una gráfica a partir del mapa de la colonia. Representamos los cruces de las calles con vértices y pondremos una arista para representar la calle que une dos cruces. Esta gráfica, construida en una pequeña región, podemos apreciarla en la Figura 3.

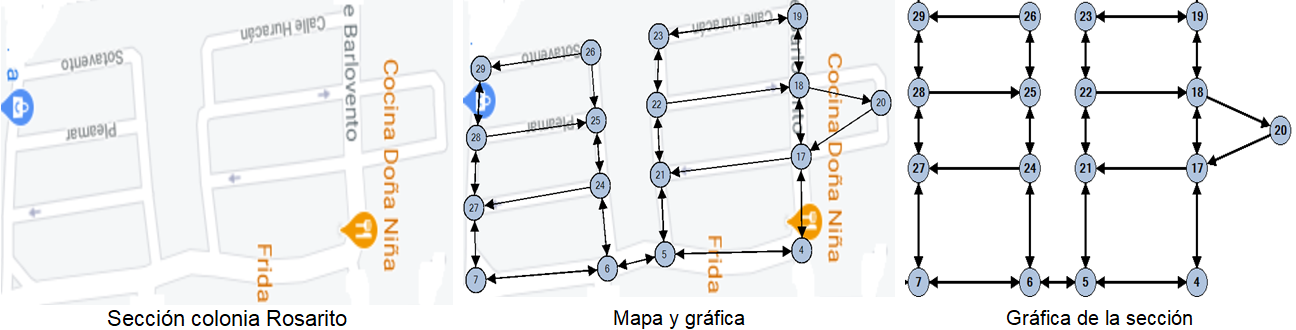
Figura 3. Construcción de la gráfica a partir del mapa de la colonia. Crédito: elaboración propia.

Nuestro problema requiere recolectar la basura casa por casa, entonces habrá que pasar por cada calle de la colonia. Idealmente, se desea pasar solo una vez, pero cuando esto no sea posible, se repetirá el paso por alguna calle. Queremos hacer esto lo menos posible para no incrementar mucho la distancia total de la ruta. Como mencionamos, la Teoría de Gráficas aborda este tipo de problemas representándolos con gráficas y usando algoritmos para construir el recorrido sobre la gráfica. Posteriormente, se realiza en la zona real, en este caso, en la colonia Rosarito.

Recorrer una gráfica es como “caminar” en ella: iniciar en un vértice, seguir por alguna de sus aristas a otro vértice, luego seguir por otra arista a otro vértice, etcétera. A esta manera de caminar le podemos poner restricciones: por ejemplo, pasar por todos los vértices de la gráfica o pasar por todas las aristas. Si “caminamos” en una gráfica, pasando exactamente una vez por cada arista, iniciando y concluyendo en el mismo vértice, obtenemos lo que se conoce como un recorrido euleriano2, y si una gráfica posee un recorrido euleriano se le llama gráfica euleriana —si no lo tiene entonces no es euleriana—. Podemos ver un ejemplo de una gráfica euleriana en la Figura 4.

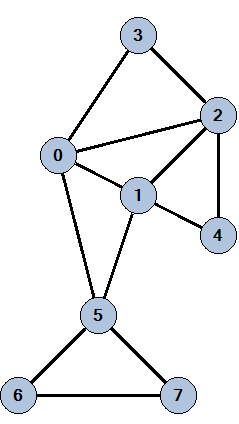
Figura 4. Gráfica euleriana. Un recorrido euleriano sería el siguiente: 0,1,2,4,1,5,7,6,5,0,2,3,0. Crédito: elaboración propia.

Entonces, una vez que construimos la gráfica de la colonia Rosarito, como dijimos antes: un vértice para cada uno de los cruces de las calles y una arista para las calles que unen dos de esos cruces, hubo que considerar algo muy importante: el sentido de las calles, porque no en todas se puede circular en los dos sentidos y un requisito es respetar las reglas de circulación.

Incorporando el sentido de las calles

Para considerar el sentido de las calles usamos flechas en las aristas. En la colonia Rosarito hay calles de un solo sentido, que representamos con una flecha en un extremo de la arista, y calles de dos sentidos representadas con flechas en ambos extremos. Esta configuración genera una digráfica, es decir, una gráfica en la que las aristas tienen dirección. Además, en la colonia también hay calles cerradas, esas en las que se entra y sale por el mismo extremo. Estas calles se deben considerar de doble sentido, dado que se entra usando un sentido y se sale usando el sentido contrario, recorriendo la misma calle. Esto implica realizar una maniobra riesgosa que llamaremos vuelta en “U”. Podemos clasificar a las vueltas en U en dos tipos diferentes: las inevitables y las evitables.

Vuelta en “U” inevitable: Se dan en las calles cerradas —sin salida— porque el camión debe entrar y salir por el mismo extremo de la calle. En la Figura 5, se muestra una calle así, es útil para entender lo complicado y peligroso de la maniobra de salida: si no hay espacio para dar vuelta al camión, el chofer sale en reversa. Ambas alternativas son riesgosas.

Figura 5. Calle cerrada en la colonia Rosarito. Crédito: elaboración propia.

Vuelta en “U” evitable: Ocurren cuando el chofer voltea el camión en una calle que no es cerrada para ahorrar tiempo o tráfico, o para ya no pasar por calles en las que ya se recolectó la basura. En el recorrido actual el chofer realiza siempre al menos una vuelta en “U” evitable. Como dijimos, con un vehículo tan grande, esta maniobra es riesgosa pues podría golpear algún auto estacionado o bloquear momentáneamente el tránsito vehicular o peatonal. La mejor ruta tendría que funcionar sin que haya necesidad de realizar este tipo de prácticas, idealmente tendríamos que eliminar todas las vueltas en “U” evitables.

Con estas consideraciones en mente, representamos la colonia Rosarito con una digráfica. Siguiendo el proceso que explicamos, asignamos vértices para cada uno de los cruces entre dos calles, aristas entre parejas de vértices que representen dos cruces unidos por una calle y flechas para indicar el(los) sentido(s) de cada calle. Las calles cerradas —que generan vueltas en “U” inevitables— se ven como una arista con flechas en sus dos extremos y que de uno de sus vértices no salen más flechas. La Figura 6 muestra la digráfica de la colonia. Por ejemplo, la arista que une a los vértices 1 y 2 representa una calle cerrada.

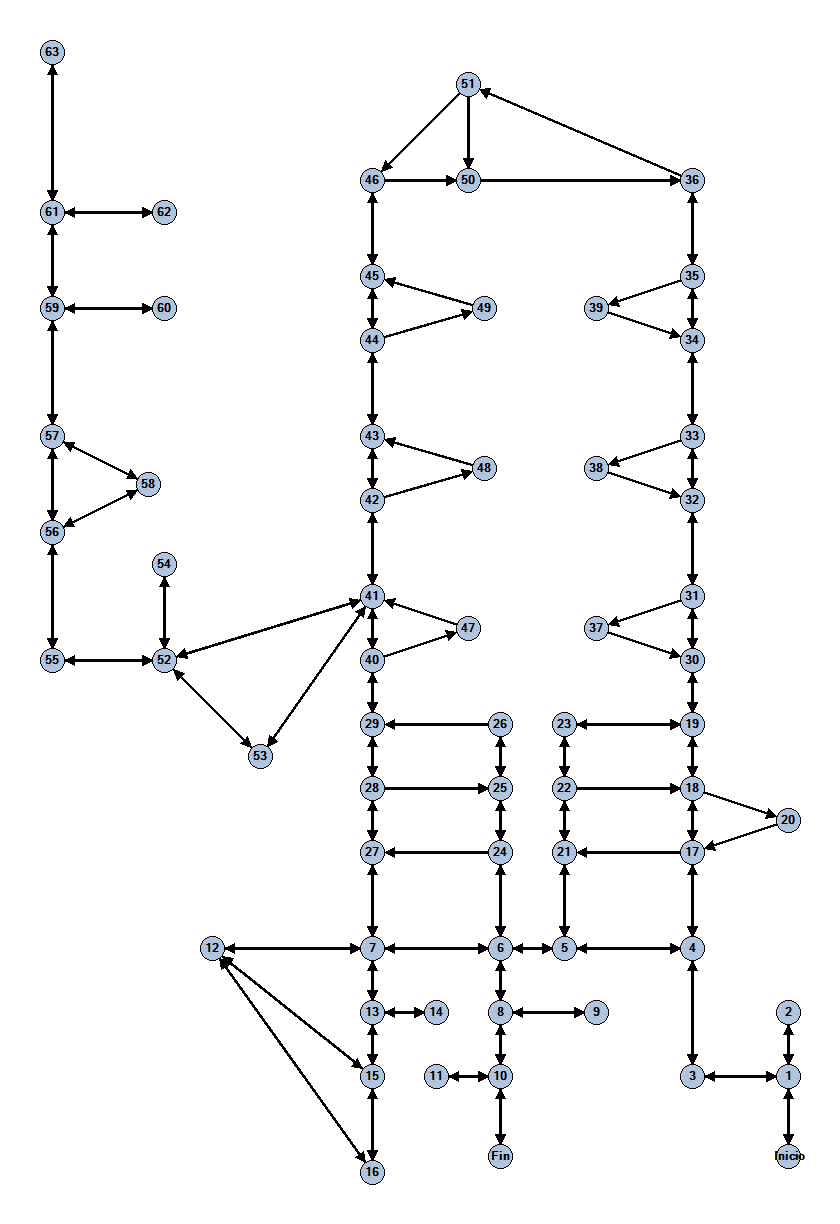
Figura 6. Digráfica que representa la colonia Rosarito. Crédito: elaboración propia.

En el caso de la gráfica de la colonia Rosarito, un recorrido euleriano representa, se vería como una ruta que pasa por cada calle una sola vez e inicia y termina en el mismo sitio. Como nosotros queremos iniciar en el almacén de las unidades recolectoras y concluir en el tiradero municipal, buscamos una trayectoria euleriana, que es como un recorrido euleriano al que se le elimina una arista. Entonces busquemos tal trayectoria.

La Teoría de Gráficas en acción

Un resultado ampliamente reconocido en la Teoría de Gráficas establece que una gráfica es euleriana si, y solo si, cada vértice está conectado por una cantidad par de aristas (Chartrand et al., 1996, 92-102). Para hallar un recorrido euleriano en una gráfica euleriana, recurrimos al algoritmo de Fleury (Fleury, 1883), presentado por el matemático francés M. Fleury en su artículo Deux problèmes de géométrie de situation en 1883. Este algoritmo encuentra un recorrido euleriano en una gráfica en la que cada vértice está unido por una cantidad par de aristas, como se ilustra en la Figura 4. ¿Podemos aplicar este algoritmo a la gráfica de la colonia Rosarito?

Al observar la Figura 6, queda claro que la gráfica no es euleriana, ya que no todos sus vértices tienen una cantidad par de aristas incidentes. Por ende, no posee un recorrido euleriano. Sin embargo, el camión recolector debe transitar por todas las calles para completar la recolección de basura. Para lograrlo, será necesario recorrer varias calles en múltiples ocasiones.

En el contexto de una gráfica, esto se representa mediante aristas múltiples, es decir, la colocación de más de una arista entre la misma pareja de vértices. Para resolver nuestro problema, añadiremos aristas nuevas para obtener una gráfica con aristas múltiples. De esta manera, garantizaremos que cada vértice tenga una cantidad par de aristas incidentes, asegurando la existencia de un recorrido euleriano. Estas aristas adicionales representarán las calles por las cuales el camión de basura pasará más de una vez. Observemos, por ejemplo, la Figura 7, en la que se agregaron dos aristas a una gráfica no euleriana, marcadas en rojo, para asegurar que todos los vértices tengan una cantidad par de aristas incidentes y así obtener una gráfica euleriana.

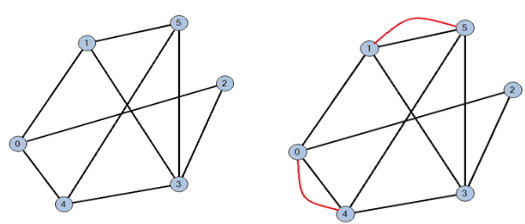
Figura 7. Adición de aristas para obtener una gráfica euleriana. Crédito: elaboración propia.

El algoritmo de Fleury no impone restricciones para eliminar las vueltas en “U” evitables. Por ejemplo, en la Figura 7 (b), el algoritmo podría seleccionar la arista negra que conecta los vértices 1 y 5, y luego, inmediatamente, la arista roja que también une los mismos vértices. En la práctica, esto implicaría que el camión recolector recorre una calle y luego la recorre en sentido contrario, realizando así una vuelta en “U” inevitable. Con el objetivo de eliminar o minimizar estas vueltas, proponemos la siguiente modificación al algoritmo de Fleury : “Si entre dos vértices u y v existen aristas múltiples, al elegir la arista de u a v, no se puede seleccionar inmediatamente la arista de v a u, a menos que no haya otra manera de regresar a u”.

En la ruta óptima, habrá calles por las que se deba transitar más de una vez, ya que la gráfica no es euleriana —como ya hemos establecido, no todos los vértices tienen una cantidad par de aristas incidentes—. Por lo tanto, se debe seleccionar cuidadosamente por cuáles calles pasar más de una vez, eligiendo aquellas que agreguen la menor distancia posible.

Para abordar esta consideración, incorporamos un dato adicional en nuestro modelo de la colonia: asignamos un número a cada arista para indicar la distancia en metros de la calle que representa. Así, obtuvimos una digráfica en la que cada arista tiene un número, como se muestra en la Figura 8.

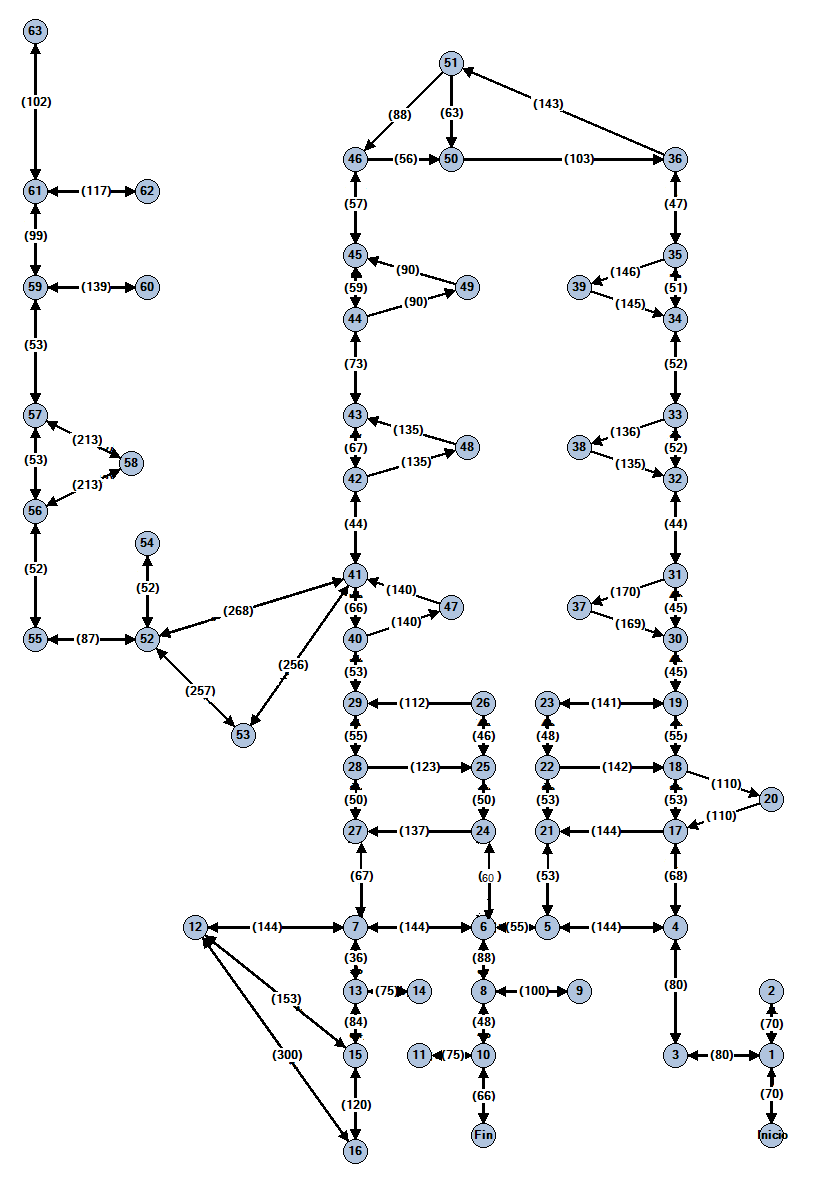
Figura 8. Digráfica de la colonia Rosarito con distancias incluidas. Crédito: elaboración propia.

Al elegir las aristas que se deben duplicar, es fundamental seleccionar aquellas que no añadan demasiada distancia a la ruta. Para lograr esto, utilizamos lo que se conoce como árbol generador de peso mínimo en una gráfica (Cormen et al., 2022, 631-642). En una gráfica, un árbol generador es una subgráfica que contiene todos los vértices de la gráfica y garantiza que entre cualquier par de vértices haya un único camino formado únicamente por aristas de ese árbol. Si, además, la gráfica tiene aristas con valores asignados (como la nuestra), llamamos árbol generador de peso mínimo a aquel cuya suma de los valores de sus aristas es la menor posible entre todos los árboles generadores de esa gráfica.

Para obtener un árbol generador de peso mínimo en nuestra gráfica, emplearemos el algoritmo de Kruskal, propuesto por el matemático estadounidense Joseph Bernard Kruskal Jr. Este algoritmo construye el árbol deseado seleccionando, entre todas las aristas de la gráfica, aquella con el menor valor asignado. Luego, elige otra de entre las aristas restantes con el menor valor, y así sucesivamente, hasta formar el árbol deseado (Kruskal, 1956). En la Figura 9, se muestra un ejemplo de árbol generador de peso mínimo, compuesto por las aristas de color rojo.

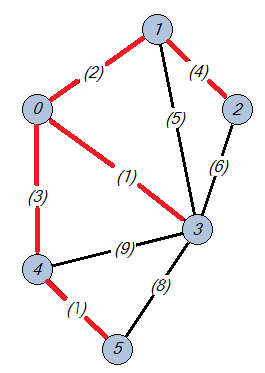
Figura 9. Árbol generador de peso mínimo obtenido con el algoritmo de Kruskal. Crédito: elaboración propia.

Es importante destacar que entre cualquier par de vértices existe un único camino formado únicamente por las aristas rojas. Además, aunque más difícil de verificar, es cierto que este es el árbol generador en el que la suma de los valores de las aristas es mínima. Por ejemplo, la arista entre los vértices 1 y 3, que tiene un valor de cinco unidades, no pertenece al árbol, ya que es posible llegar del vértice 1 al 3 usando dos aristas: la que va del 1 al 0 y la que va del 0 al 3. La suma de esos valores es tres, que es menor que el valor de la arista entre 1 y 3.

Las aristas de un árbol generador de peso mínimo en nuestra gráfica son aquellas de las que elegimos duplicar, ya que, al tener los valores más pequeños, representan calles más cortas. Si el camión recolector pasa más de una vez por ellas, no se incrementa tanto la distancia, logrando así optimizar nuestra ruta.

Conclusiones

Tras aplicar los algoritmos mencionados, obtuvimos una ruta con una distancia total de 10.972 km, en comparación con los 11.677 km de la ruta actual. Esto implica una mejora de 0.695 km, es decir, 695 metros. Esta reducción se traduce en un ahorro semanal de 2.085 kilómetros, considerando que la ruta se realiza tres veces a la semana. Por tanto, el ahorro anual al sustituir la ruta actual por esta nueva sería de aproximadamente 108.718 kilómetros. La Figura 10 es una animación (un gif) que muestra la ruta óptima obtenida en la digráfica que representa a la colonia Rosarito.

Cuando una arista cambia a color rojo, significa que el camión recolector de basura debe pasar por la calle que esa arista representa. Si la arista cambia a color amarillo, el camión debe pasar una segunda vez, y si cambia a color negro, entonces deberá recorrerla tres veces.

Figura 10. La ruta completa del camión recolector en la colonia Rosarito. Crédito: elaboración propia.

En la ruta que proponemos, no existen vueltas en “U” evitables, logrando que, además de ser más corta, sea más segura. Esta estrategia podría replicarse en otras colonias y sistemas de recolección que cumplan con las características de este problema, mejorando así las rutas de recolección de basura en otras zonas del país.

Referencias

• Chartrand, G., Lesniak, L., y Zhang, P. (2010). Graphs & Digraphs. En Chapman and Hall/CRC eBooks. https://doi.org/10.1201/b14892.
• Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms, third edition. mit Press. https://pd.daffodilvarsity.edu.bd/course/material/book-430/pdf_content.
• Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical society, 7(1), 48-50. http://5010.mathed.usu.edu/Fall2018/THigham/Krukskal.pdf.
• Martínez Cano, O. (2021). Uso de la Teoría de Gráficas para optimizar la ruta de recolección de basura en la colonia Rosarito del municipio de Los Cabos. [Tesis de licenciatura, en proceso de publicación]. Universidad Abierta y a Distancia de México, unadm.
• Wikipedia. (2021, 4 de diciembres). Discusión: problema de los puentes de Königsberg. https://goo.su/YCUxsd.

Recepción: 15/12/2022. Aceptación: 01/11/2023.