Probabilidad y estadística en la toma de decisiones
Vol. 25, núm. 2 marzo-abril 2024
Probabilidad y estadística en la toma de decisiones
Alan David Ramírez Noriega, Carolina Tripp-Barba y Samantha Paulina Jiménez Calleros CitaResumen
La probabilidad y estadística son áreas de estudio que tienen su origen en el siglo xvi y que se han desarrollado a lo largo de la historia. La probabilidad se refiere al grado de certeza de que un suceso ocurra o no, mientras que la estadística se encarga de recopilar y analizar datos para generar explicaciones y predicciones. Estas disciplinas se aplican en diferentes ámbitos. Algunos ejemplos de sus aplicaciones son predecir el clima, conocer qué equipo de fútbol ganará el mundial o el comportamiento de las inversiones en la bolsa de valores. Además, ante el incremento de la información, se han desarrollado sistemas más complejos para diagnosticar enfermedades, asignar precio a pólizas de seguros o la construcción de coches autónomos. En este artículo hablamos de estos temas a mayor profundidad.
Palabras clave: incertidumbre, probabilidad, estadística, toma de decisiones, Bayes.
Probability and statistics in decision making
Abstract
Probability and statistics are areas of study that originated in the 16th century and have developed throughout history. Probability refers to the degree of certainty that an event will occur, while statistics is responsible for collecting and analyzing data to generate explanations and predictions. These disciplines are applied in different fields. Some examples of applications of probability and statistics are predicting the weather, knowing which soccer team will win the World Cup or the behavior of investments in the stock market. Furthermore, given the increase in information, more complex systems have been developed to diagnose diseases, assign a price to insurance policies, or build autonomous cars. In this article we talk about these topics in greater depth.
Keywords: uncertainty, probability, statistics, decision making, Bayes.
Introducción
A partir del siglo xvi se comenzaron a estudiar muchos fenómenos que seguían patrones aleatorios y eran inciertos, por lo tanto, difíciles de predecir. Blaise Pascal y Pierre de Fermat desarrollaron la teoría de probabilidad para dar respuesta a este tipo de situaciones. Muchos otros investigadores tales como Bernoulli, Bayes, Lagrange, Laplace, Gauss y Poisson, por mencionar algunos, siguieron desarrollando esta ciencia (Restrepo y González, 2003). Alguien que toma decisiones debe de ser consciente que la variabilidad está en muchas áreas relacionadas a esa decisión, por lo que la probabilidad y estadística ayudan a enfrentar ese riesgo.
Según la teoría de incertidumbre, una afirmación no es verdadera o falsa, sino que hay ciertas expectativas de que sea una u otra. Generalmente, esta incertidumbre se debe a la falta de un conocimiento absoluto sobre los hechos y las leyes que rigen dicho fenómeno (Gómez-Romero et al., 2014).
El estudio de la incertidumbre genera un interés genuino en el ser humano y se utiliza para diferentes aspectos cotidianos como predecir el clima, conocer qué equipo de fútbol ganará el mundial o el comportamiento de las inversiones en la bolsa de valores. La predicción del futuro para tomar decisiones siempre ha despertado interés, es por eso que desarrollar una ciencia que apoye a los seres humanos en estas situaciones ha cobrado tanta popularidad (Gutiérrez y Vladimirovna, 2014).
La probabilidad y la estadística son dos áreas de estudio independientes pero ligadas comúnmente, por su facilidad de acoplamiento. La probabilidad se define como el grado de certeza de que ocurra o no un suceso. La estadística se encarga de obtener y analizar datos para generar explicaciones y predicciones (Anderson et al., 2008).
La estadística es tan importante que la Organización de la Naciones Unidas (onu) estableció, a partir del 2010, que el 20 de octubre se conmemore el día mundial de la estadística (Naciones Unidas, 2023); como dato curioso el día se celebra cada cinco años. La estadística se emplea comúnmente en estudios demográficos, económicos, políticos, sociales y científicos por lo que su estudio y aplicación se vuelven indispensables para la toma de decisiones en la vida diaria. En la siguiente sección se describen algunos ejemplos donde se aplica la probabilidad y estadística.
Aplicaciones de la probabilidad y estadística
Un ejemplo del uso de la probabilidad y la estadística es el de medir la intención de voto de las personas, con ellas se pueden hacer predicciones para conocer el posible candidato ganador. Esto es muy importante para los partidos políticos, ya que permite generar datos para tomar decisiones. Así, candidatos a la baja podrían establecer campañas más activas para tratar de recuperar votantes.
Asimismo, las compañías de seguro, de manera general, basan el precio de sus pólizas de acuerdo con la probabilidad y estadística. Por ejemplo, estas compañías llevan registro de los robos y choques de autos, de tal forma que, si el vehículo tiene un alto índice de robos, su póliza será más alta que otros con un índice menor.
La probabilidad y estadística se aplican también en la esperanza de vida de la población, éste es un factor importante en un país, ya que representa la media de años que una persona puede vivir. En México para 2023, la esperanza de vida de las mujeres fue de 78.6 años y en los hombres 72.3 años, de acuerdo con el Instituto Nacional de Estadística y Geografía (inegi, 2023). Estos valores son útiles porque describen el nivel de desarrollo de una población, es decir, tener una esperanza de vida alta indica niveles de vida adecuados, pues la población tiene una vida larga y saludable. La probabilidad y estadística permiten medir estos factores y predecir tendencias sobre ellos. Así, el gobierno puede estar preparado para incrementar los servicios para personas mayores, tales como hospitales, medicinas o apoyos económicos, si fuese necesario.
Los ejemplos anteriores son aplicaciones de la probabilidad y estadística desde hace muchos años, en las que el cálculo se podía hacer con lápiz y papel utilizando las fórmulas desarrolladas en estas ciencias. Después, con la aparición de la tecnología, la obtención de estas predicciones se transformó debido al uso de calculadoras potentes y computadoras, así como hojas de cálculo o software especializado en estas áreas.
Aún más, debido al crecimiento exponencial de los datos, los medios tecnológicos antes mencionados quedaron rebasados y no fueron suficientes para el procesamiento y análisis de la información. Fue así que los sistemas de cómputo inteligente y las técnicas de inteligencia artificial tomaron tanta relevancia en los últimos años (Nasteski, 2017). Estos son algunos ejemplos de aplicaciones de sistemas inteligentes en la probabilidad y estadística.:
- Detección de enfermedades. Uno de los primeros usos fue el diagnóstico de enfermedades. Este tipo de predicción se dan con base en datos del paciente, tales como síntomas, sexo, edad, historial clínico, entre otros, estas variables son analizadas para determinar la probabilidad de una determinada enfermedad. Esto brinda mayor rapidez en el diagnóstico de un padecimiento. Cabe destacar que este tipo de sistemas son apoyo a la toma de la decisión para profesionales y no son aptos para autodiagnósticos.
- Clasificación de correo spam. El spam es correo que llega a la cuenta de un usuario y que no tiene un beneficio para él, se considera correo basura, y generalmente son ofertas, invitaciones a usar aplicaciones, suscripciones a sitios, intentos de extorsión, entre otros. Este tipo de correo puede ser molesto cuando llega en grandes cantidades, por lo que las aplicaciones de correo como Outlook o Gmail filtran la recepción de estos mensajes enviándolos a la sección de correos no deseados. Hay diferentes formas de detectar el spam, una de ellas es que las aplicaciones tienen registros de correos spam, y los usuarios ayudan con esta clasificación de forma manual. Cuando un correo nuevo llega a la cuenta, este correo es analizando con base en las palabras que contiene, si hay muchas que coincidan con el correo spam ya detectado, es probable que este nuevo también lo sea, por lo que se clasifica como correo basura. Aun así, los usuarios verifican la clasificación de correo y pueden recuperar correos asignados a esta categoría.
- Toma de decisiones en vehículos autónomos. Un vehículo autónomo implica el desarrollo de un sistema complejo1 que pretende realizar las mismas funciones que hace un coche convencional, pero sin intervención humana. Dentro de este sistema, una de las partes más importante son los algoritmos de toma de decisiones, ya que éstos permitirán dotarlos de información de experiencias previas para configurar su respuesta y comportamiento en tiempo real, o sea, le proporcionará al auto la capacidad de ir aprendiendo, lo que le permitirá tomar decisiones en décimas de segundos (como lo haría un conductor). Lo anterior es gracias a que será programado con información que le permita discriminar y evaluar situaciones de riesgo, como cambiar de carril, desviarse, evitar peatones, etcétera. Sin embargo, debido a las lagunas legales que introduce el hecho de que estas decisiones las tome una máquina, la entrada de este tipo de vehículos (totalmente autónomos) al mercado ha sido un poco más lenta de lo esperado (Valero-Matas y De la Barrera, 2020).
- Detección de clientes que no pagarán un crédito. Las empresas que se dedican a dar préstamos de dinero están interesadas en saber si los clientes pagarán la ayuda otorgada. Así, pueden evitar autorizar los préstamos a personas con características relevantes y similares a quienes no saldaron su crédito. Estas características pueden ser número de hijos, salario, deudas, monto del préstamo, casa propia, entre otros.
La probabilidad y estadística en detalle
Para explicar a mayor profundidad la forma en que se aplica la probabilidad y estadística, se brinda el siguiente ejemplo basado en la detección de clientes que no pagarán el crédito. En la tabla 1 se muestra la base de conocimiento, es decir, el histórico de clientes con sus atributos (datos) y si devolvieron el crédito o no. Estas bases de datos son de millones de registros, pero para fines explicativos sólo se muestran 5 casos. Las características consideradas son el salario (bajo, medio, alto), la edad (joven, mayor), el préstamo (bajo, medio, alto) y si devuelve el crédito (si, no).
| Id | Salario | Edad | Préstamo | Dev. créd. |
|---|---|---|---|---|
| 1 | Alto | Mayor | Medio | Si |
| 2 | Alto | Joven | Bajo | Si |
| 3 | Medio | Joven | Alto | No |
| 4 | Bajo | Joven | Bajo | Si |
| 5 | Bajo | Mayor | Medio | No |
Tabla 1. Ejemplo base de conocimiento.
El algoritmo representa el motor de inferencia, esto significa, la probabilidad y estadística aplicada para determinar matemáticamente si es buen cliente o no. De acuerdo con el ejemplo, tenemos un nuevo cliente con salario bajo, joven y que solicita un préstamo medio (ver figura 1). La cuestión es: ¿la empresa debe otorgar el préstamo al cliente?
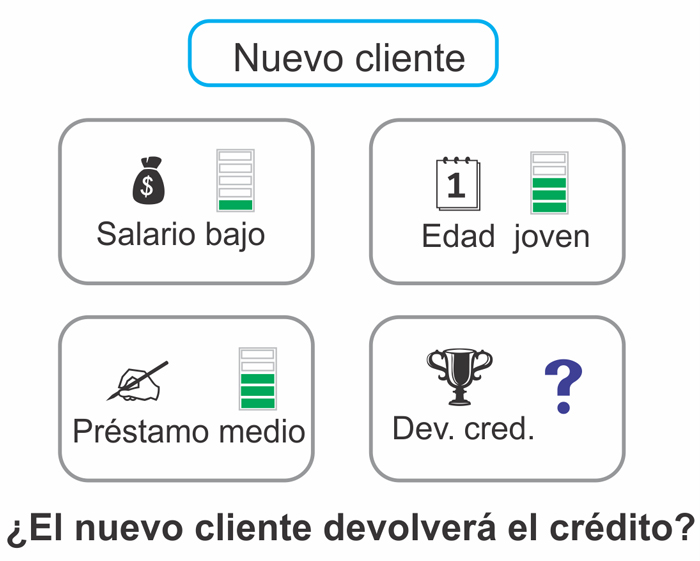
Figura 1. Representación del nuevo cliente.
Crédito: elaboración propia.
La lógica de decisión está representada en la figura 2. El proceso indica el cálculo de probabilidades para un buen cliente (sí devuelve el crédito) y un mal cliente (no devuelve el crédito). La probabilidad mayor será tomada como la decisión recomendada.

Figura 2. Lógica de decisión.
Crédito: elaboración propia.
El algoritmo considera tomar las características del nuevo cliente y buscar las coincidencias en la base de conocimiento. Es decir, se considera el salario del nuevo cliente, el cual es bajo, y se buscan cuántos clientes hay con salario bajo y si devolvieron el crédito. Según la búsqueda, hay un cliente de tres (1/3) que si devolvió el crédito. Igualmente se aplica con la edad (2/3) y con el préstamo (1/3), todo lo obtenido se multiplica considerando la proporción de clientes que si devolvieron el crédito del total de registros de la base de conocimiento (3/5). Esto brinda un 0.044 de probabilidades de que el cliente con los atributos en la figura 2 devuelva el crédito.
El mismo procedimiento se aplica para calcular la probabilidad de que el cliente no devuelva el crédito. Este cálculo arroja una probabilidad de 0.050. Convirtiendo el dato en porcentaje a través de la normalización, es decir, sumando ambos valores obtenidos y obteniendo la proporción individual de los valores. Así, tenemos un 46.81% (0.044) y un 53.19% (0.050). O sea, la probabilidad determina que hay un 53.19% de que el cliente no devuelva el préstamo, contra un 46.81% de que sí lo haga. La decisión es muy cerrada, sin embargo, el sistema recomienda rechazarlo, ya que sus características están más cercanas a las personas que no devuelven el crédito. Como en todo sistema de apoyo a la decisión, el usuario que manipula el sistema toma la decisión final.
Este algoritmo se llama Bayes ingenuo, es de los primeros sistemas que surgieron para predicción, y es muy efectivo aun cuando su procesamiento sea muy simple. El algoritmo está basado en el teorema de Bayes propuesto por el matemático Thomas Bayes en el siglo xviii (Stylianides y Kontou, 2020).
Como se aprecia en el procedimiento, este algoritmo supone independencia entre los atributos (Hernández et al., 2004), es decir, no considera una relación entre el salario y la edad, de ahí se deriva la palabra ingenuo. Por lógica, se podría pensar que una persona con muchos años laborales tendría mejores oportunidades de crecimiento y por lo tanto mejor salario; sin embargo, aunque el algoritmo considera que los atributos son independientes, es competitivo en cuanto a rendimiento contra otros algoritmos. El algoritmo de Bayes ingenuo fue presentado aquí resumiendo muchas de sus funcionalidades, sin embargo, se logra ejemplificar su forma de trabajo. El algoritmo explicado es solo un método para el apoyo a la toma de decisiones, sin embargo, existen otros métodos basados en estadística como: regresión logística, redes bayesianas o arboles de decisión (Ghahramani, 2015).
Conclusiones
La probabilidad y estadística son útiles en la toma de decisiones cuando no hay certeza en cómo se comportarán los eventos. Quien toma las decisiones debe de ser consciente de que la variabilidad está presente en muchas áreas relacionadas con la decisión, por lo que la probabilidad y estadística ayudan a enfrentar este riesgo. Las decisiones no se deben tomar por intuición, sino basadas en datos históricos relacionados con la problemática, de tal forma que, la decisión tenga el mayor margen de éxito.
Tal como se muestra en el artículo, está área matemática puede ser aplicada a diversos campos; sin embargo, requiere desarrollar pensamiento matemático para ser empleada adecuadamente. En la investigación, la estadística inferencial es ampliamente usada para la experimentación y la prueba de hipótesis, por lo que ha sido vital en el desarrollo de la ciencia. La probabilidad y estadística es un área de estudio muy importante ya que brinda una visión para la toma de decisiones y un análisis del pasado para predecir el futuro.
En los tiempos actuales, la ciencia de datos2 tiene un enfoque multidisciplinario, sin embargo, toma muchas bases de la probabilidad y estadística, por lo que tener conocimientos en estas dos áreas cobra particular importancia para diseñar y aplicar modelos predictivos que puedan resolver problemas cotidianos y mejoren la calidad de vida del ser humano.
Referencias
- Anderson, D., Sweeney, D., y Williams, T. (2008). Statistics for Business and Economics (10a. ed.). Thomson/Southwestern.
- Ghahramani, Z. (2015) Probabilistic machine learning and artificial intelligence. Nature 521, 452–459. https://doi.org/10.1038/nature14541.
- Gómez-Romero, J., García, J., y Molina, J. M. (2014). Modelos de Representación de Imprecisión e Incertidumbre en Fusión de Alto Nivel. xvii Congreso Español Sobre Tecnologías y Lógica Fuzzy (ESTYLF), Zaragoza, España. https://bisite.usal.es/archivos/2014_estylf.pdf.
- Gutiérrez, E., y Vladimirovna, O. (2014). Probabilidad y estadística. Aplicaciones a la ingeniería y las ciencias (1ª. ed.). Grupo Editorial Patria.
- Hernández, J., Ramirez Ma. J., y Ferri C. (2004). Introducción a la minería de datos. Pearson Educación.
- Instituto Nacional de Estadística y Geografía (inegi). (2023, 6 de octubre). Esperanza de vida al nacimiento por entidad federativa según sexo, serie anual de 2010 a 2023. http://tinyurl.com/23fdccr4.
- Naciones Unidas. (2023, 9 de octubre). Día Mundial de la Estadística. https://www.un.org/es/observances/statistics-day.
- Nasteski, V. (2017). An overview of the supervised machine learning methods. Horizons, 4, 51-62. https://doi.org/10.20544/HORIZONS.B.04.1.17.P05.
- Restrepo B., L. F., y González L., J. (2003, marzo). La Historia de la Probabilidad. Revista Colombiana de Ciencias Pecuarias, 16(1), 83-87. https://www.redalyc.org/pdf/2950/295026121011.pdf.
- Stylianides N., y Kontou E. (2020). Bayes Theorem and its Recent Applications. Mathematics Research Journal, 2. https://journals.le.ac.uk/ojs1/index.php/lumj/article/view/3488/3130
- Valero-Matas, J. A., y De la Barrera, A. (2020). The Autonomous Car: A better future? Sociología y tecnociencia, 10(1), 136-158. https://revistas.uva.es/index.php/sociotecno/article/view/4225


